Regular Polygon - Definition, Examples, Quiz, FAQ, Trivia
Learn about shapes with equal sides and angles through examples and activities
What is a Regular Polygon?
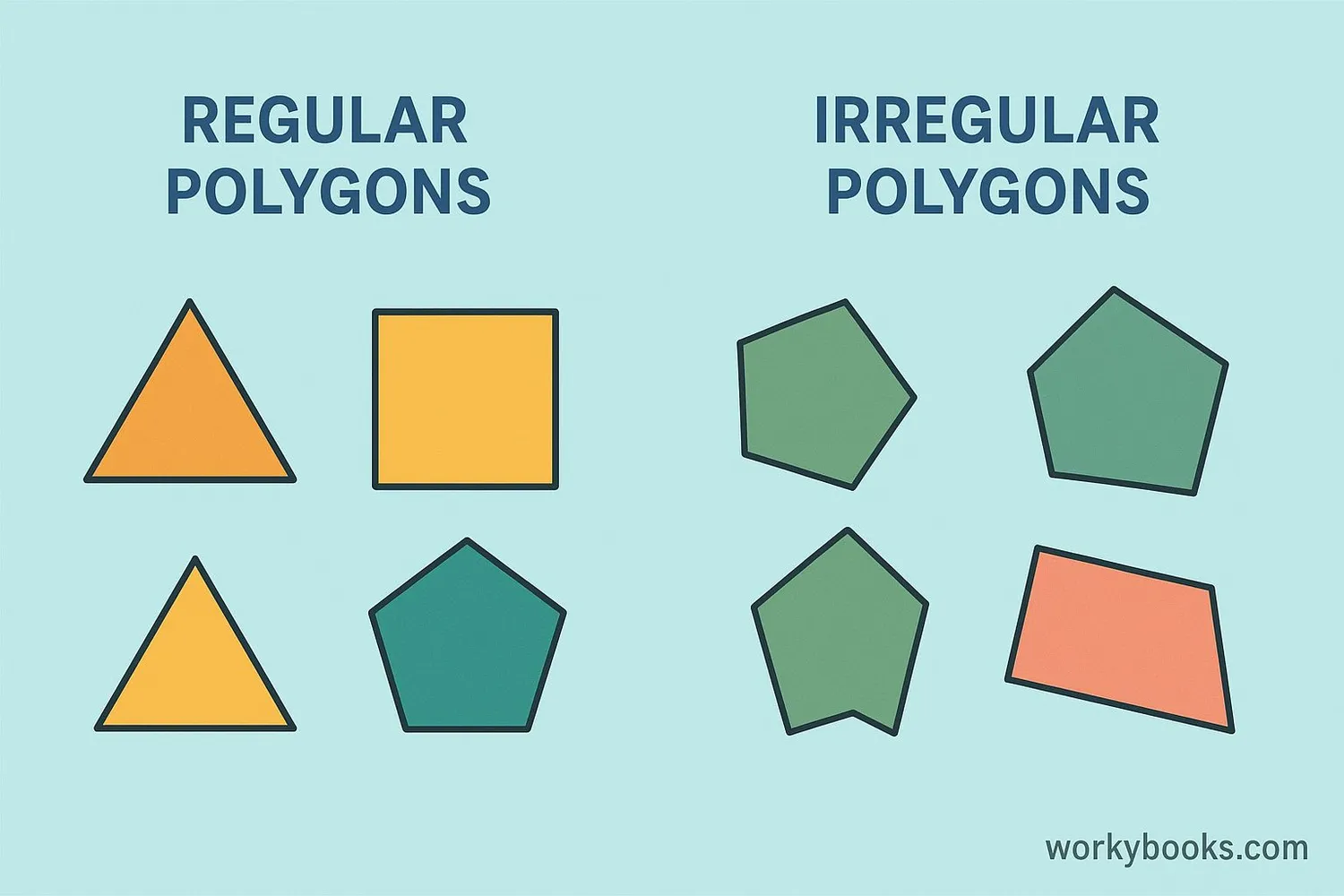
A regular polygon is a special shape where all sides are the same length and all angles are equal. Think of it like a perfectly balanced shape!
For example, a square has four equal sides and four equal angles (each 90 degrees). An equilateral triangle has three equal sides and three equal angles (each 60 degrees).
Regular polygons are different from irregular polygons. Irregular polygons have sides of different lengths or angles of different sizes. A rectangle that isn't a square is irregular because its sides aren't all equal, even though its angles are.
Key Concept
For a polygon to be regular, it must have two things: all sides equal and all angles equal.
Properties of Regular Polygons
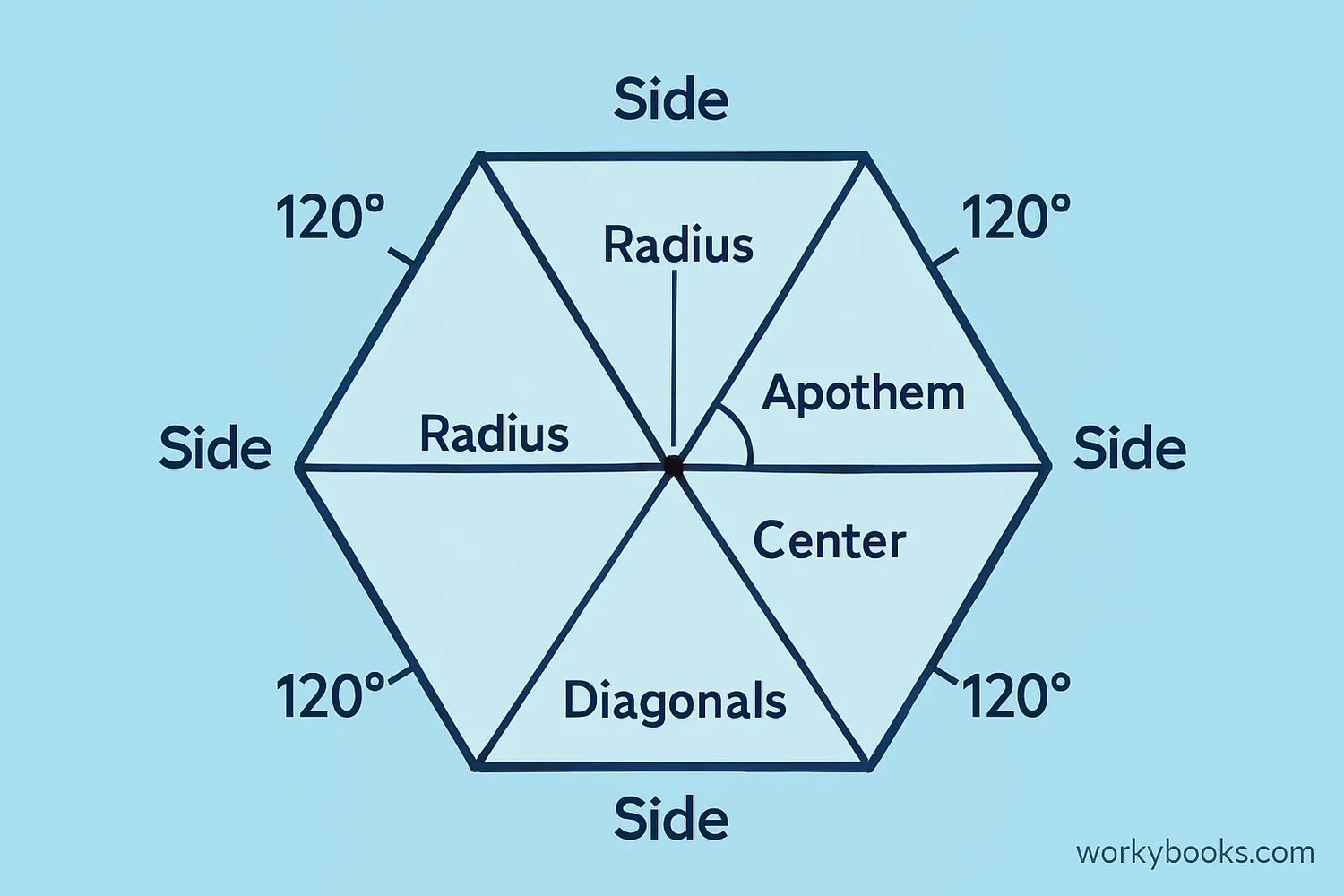
Regular polygons have special properties that make them interesting to study:
Equal Sides: All sides have exactly the same length.
Equal Angles: All interior angles are exactly the same size.
Symmetry: Regular polygons have rotational symmetry and reflection symmetry.
Circumcircle: A circle can be drawn that passes through all vertices (corners) of the polygon.
Incircle: A circle can be drawn inside the polygon that touches all sides.
The number of sides determines the name of the polygon. For example, a polygon with 5 sides is called a pentagon, and if it's regular, we call it a regular pentagon.
Remember
The more sides a regular polygon has, the more it looks like a circle!
Types of Regular Polygons
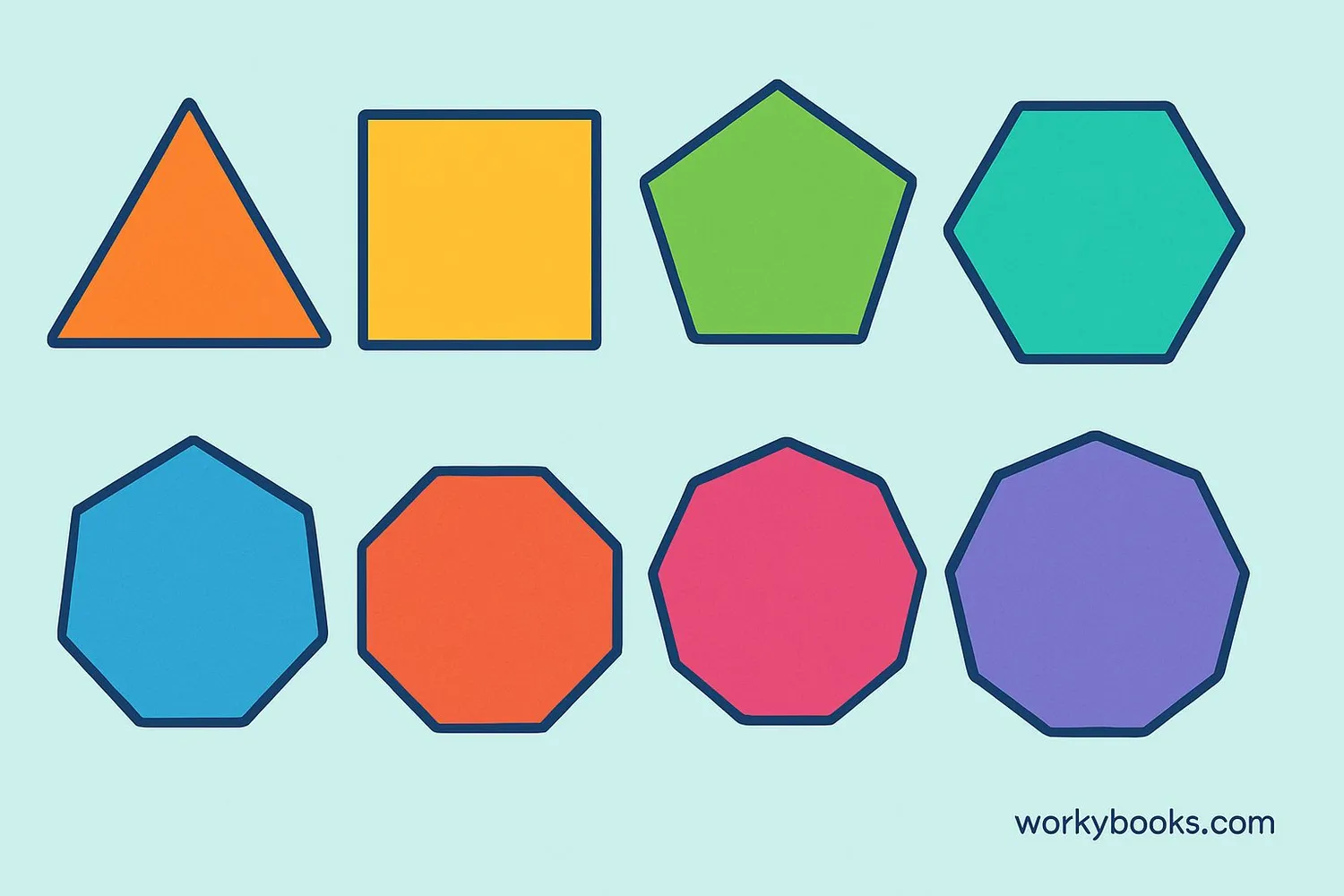
Regular polygons are named based on how many sides they have. Here are some common regular polygons:
Triangle
3 sides
Square
4 sides
Pentagon
5 sides
Hexagon
6 sides
Octagon
8 sides
Circle
Infinite sides
Notice how each polygon has its own unique look, but they all follow the same rule: equal sides and equal angles. The circle is a special case - it's like a polygon with infinitely many sides!
Fun Fact
Honeybees build their hives with regular hexagons because this shape uses the least wax to hold the most honey!
Formulas for Regular Polygons
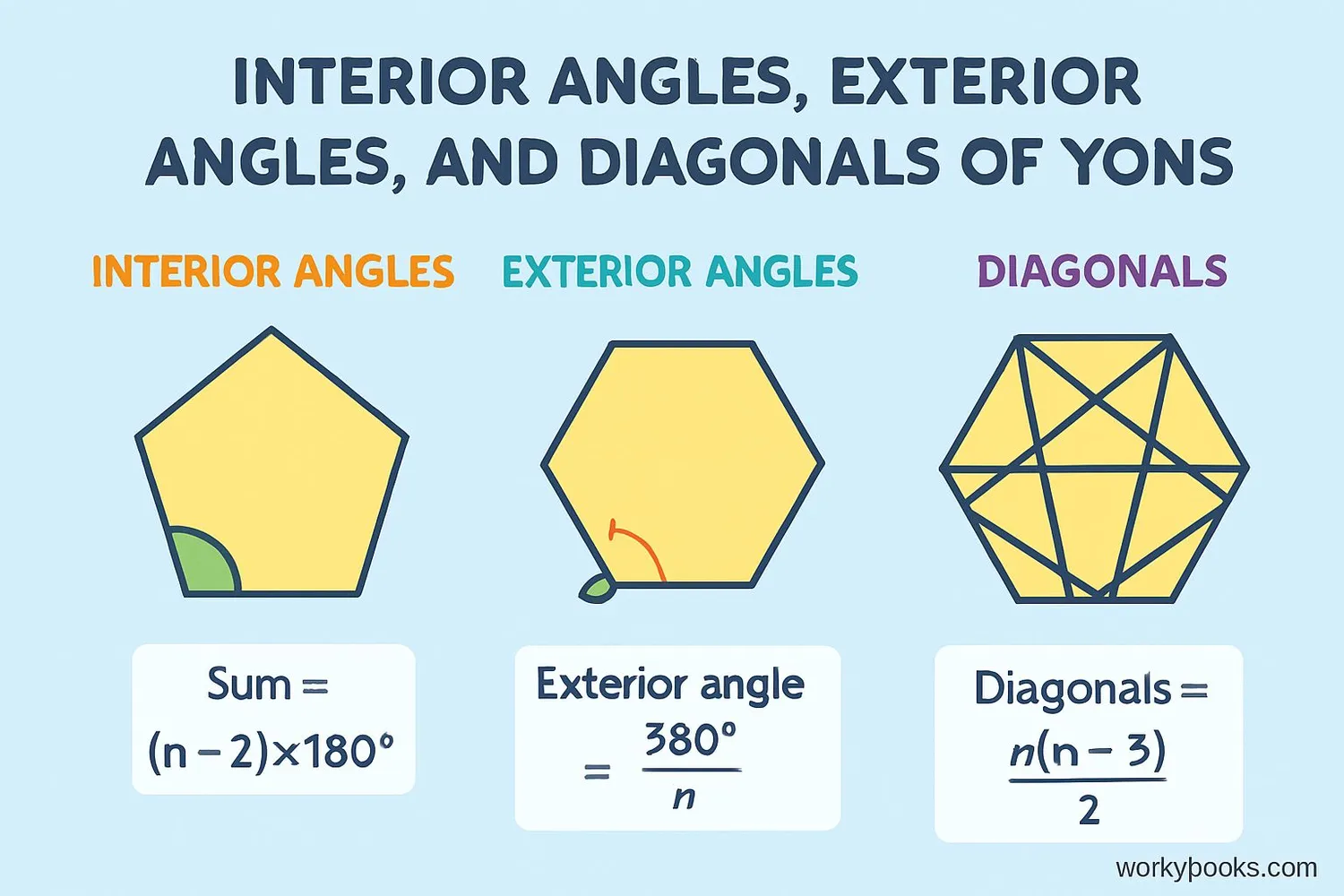
We can calculate interesting properties of regular polygons using these formulas:
Sum of Interior Angles
Where n is the number of sides
Each Interior Angle
For regular polygons only
Each Exterior Angle
Same for all regular polygons with n sides
Number of Diagonals
Diagonals connect non-adjacent vertices
Let's try an example: For a regular pentagon (5 sides):
Sum of interior angles = (5-2) × 180° = 540°
Each interior angle = 540° ÷ 5 = 108°
Each exterior angle = 360° ÷ 5 = 72°
Number of diagonals = 5(5-3) ÷ 2 = 5 diagonals
Remember
For any polygon, the sum of exterior angles is always 360°, no matter how many sides it has!
Polygon Practice Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about regular polygons:
Geometry Trivia
Discover interesting facts about polygons and shapes:
Nature's Hexagons
Honeybees build their hives in hexagonal patterns because this shape allows them to store the most honey while using the least amount of wax. Hexagons fit together perfectly with no gaps!
Ancient Architecture
The ancient Greeks were fascinated with regular polygons. The Parthenon in Athens uses the golden ratio found in pentagons, and many Greek buildings feature octagonal designs.
Snowflake Science
All snowflakes have hexagonal symmetry because of how water molecules arrange themselves when freezing. This creates their beautiful six-sided patterns that are never exactly alike!
Strong Shapes
Triangles are the strongest polygon, which is why they're used in bridges and towers. Hexagons are also very strong, which is why they're used in soccer balls and nuts/bolts.





