Scale Factor - Definition, Examples, Quiz, FAQ, Trivia
Learn how shapes grow and shrink with this important math concept
What is Scale Factor?
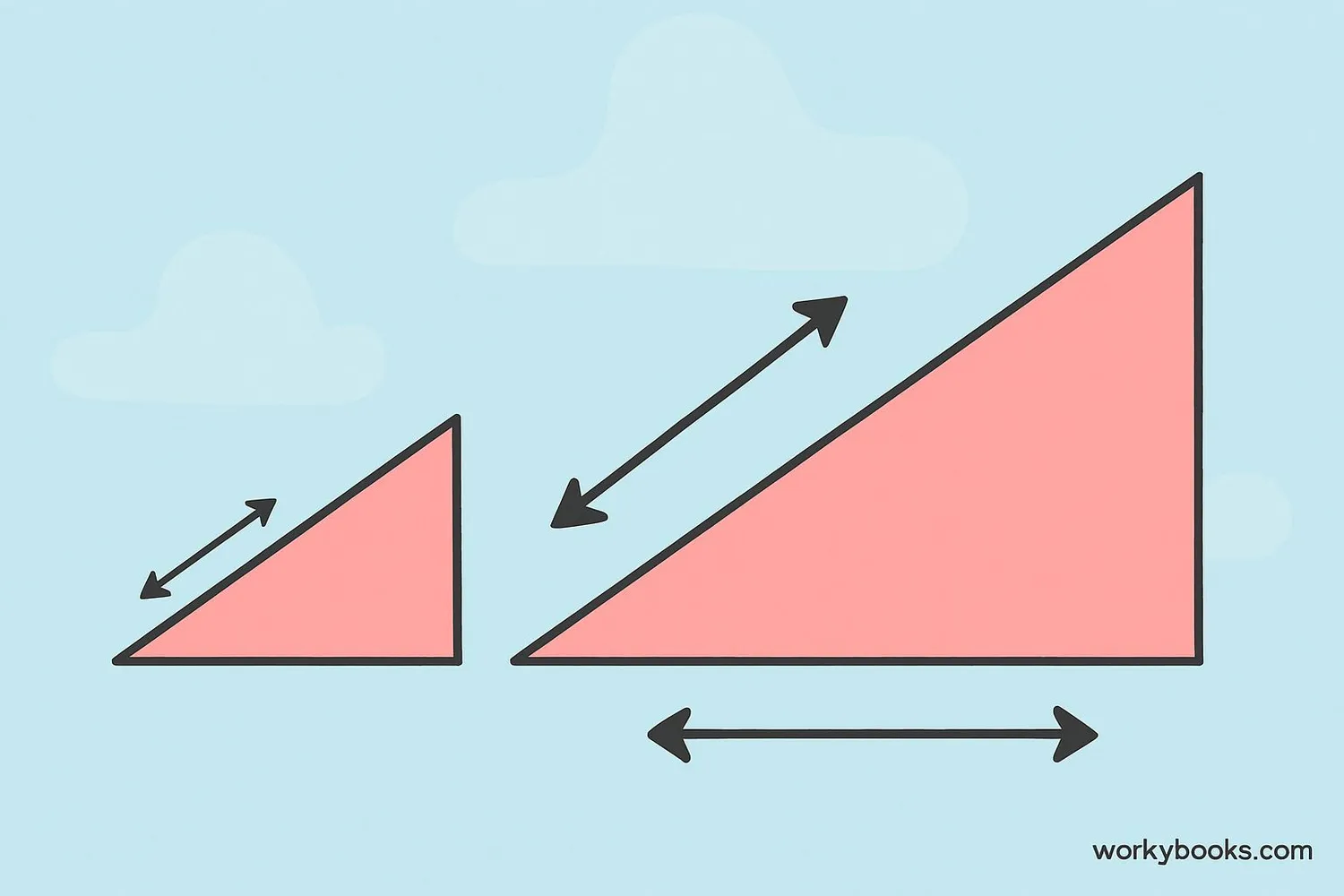
A scale factor is a special number that tells us how much bigger or smaller a shape has become. It's like a magic number that can make shapes grow or shrink!
Definition: Scale factor is the ratio between the measurements of two similar shapes. When we multiply all the sides of a shape by the same scale factor, we get a new shape that looks the same but is a different size.
Think about zooming in on a picture on your tablet. That zoom effect uses scale factor to make everything bigger. Or when you see a toy car that's a smaller version of a real car - that also uses scale factor!
Key Concept
Scale factor > 1 = Enlargement (makes shapes bigger)
Scale factor < 1 = Reduction (makes shapes smaller)
How to Find Scale Factor
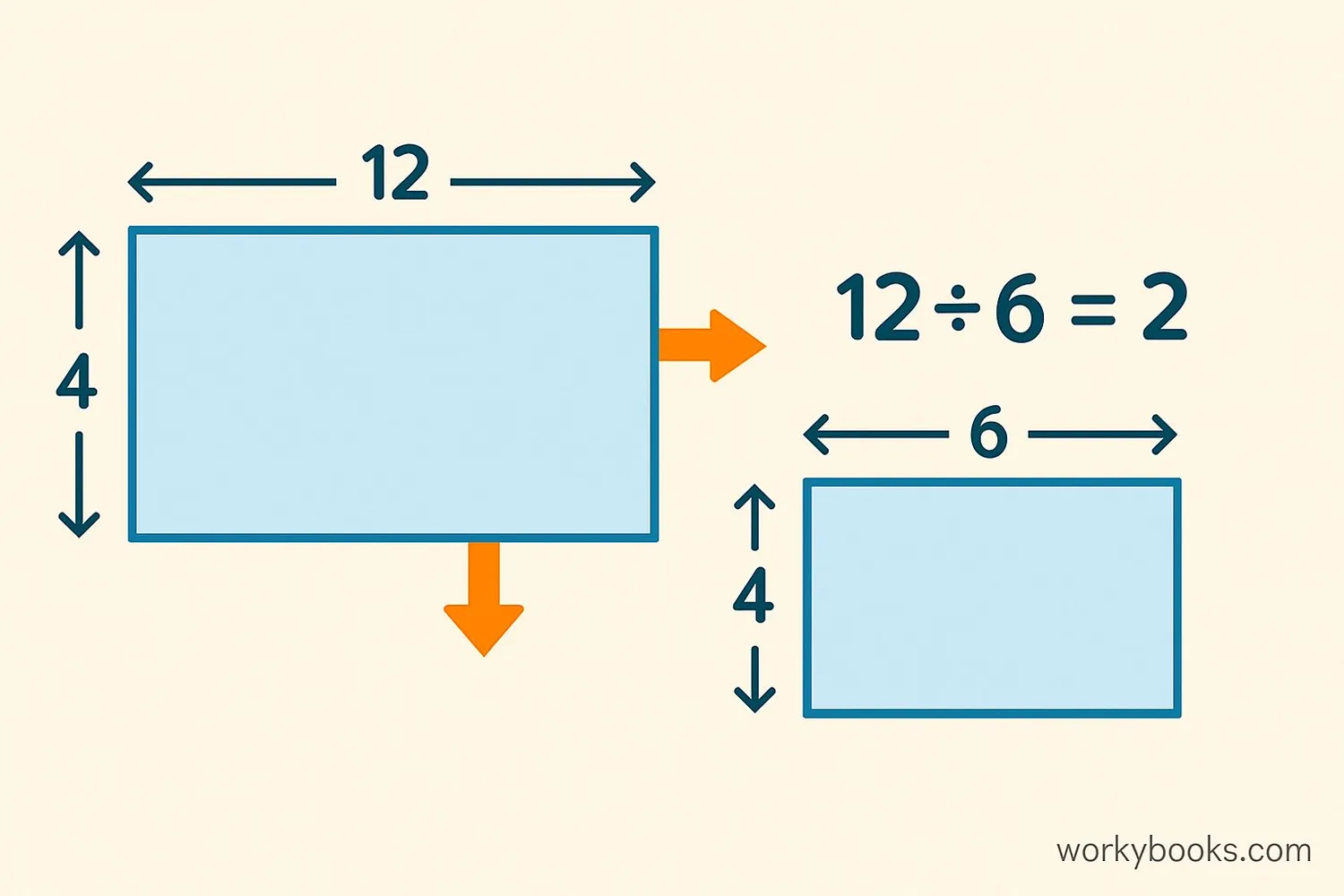
Finding scale factor is like solving a puzzle! Here's how you do it:
1. Find two corresponding sides from the original and new shape.
2. Divide the length of the new shape's side by the original shape's side.
3. That number is your scale factor!
Example: If a small triangle has a side of 3 cm, and the bigger similar triangle has a corresponding side of 6 cm, the scale factor is:
6 cm ÷ 3 cm = 2
This means every side of the bigger triangle is twice as long as the small one.
Remember
Always divide the NEW measurement by the ORIGINAL measurement to find the scale factor.
Scale Factor Formula

The formula for scale factor is simple and easy to remember:
Scale Factor Formula
This formula works for any dimension - length, width, or height!
Example: A model house is 15 cm tall. The real house is 900 cm tall. What's the scale factor?
Solution: Scale Factor = 15 cm ÷ 900 cm = 1/60
This means the model is 60 times smaller than the real house. Every 1 cm on the model represents 60 cm on the real house.
Scale Factor in Similar Figures
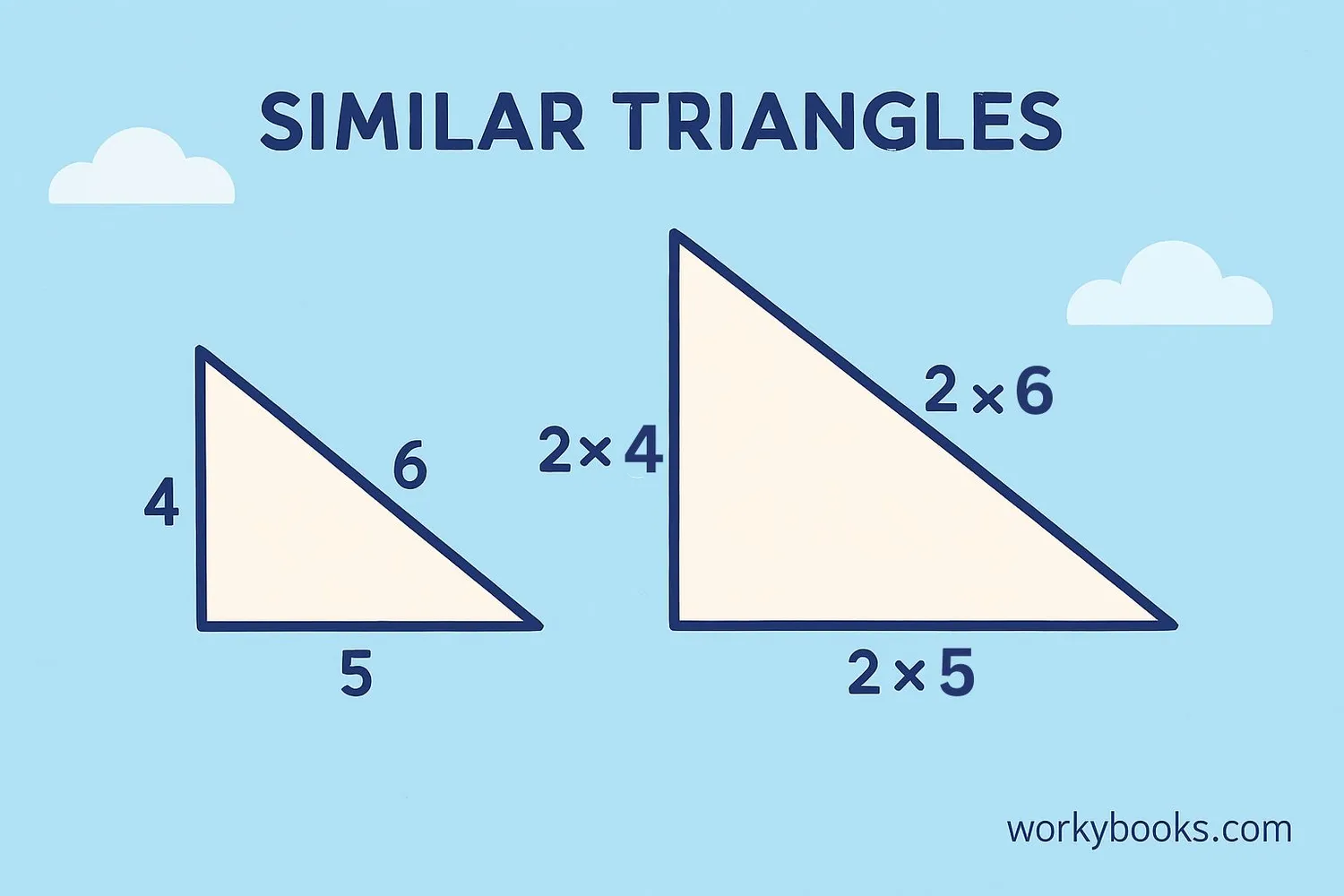
Similar figures are shapes that look exactly alike but are different sizes. They have the same angles and their sides are proportional. This is where scale factor becomes really important!
Key facts about similar figures:
- All corresponding angles are equal
- Corresponding sides are proportional
- The ratio of any two corresponding sides is the scale factor
Enlargement
Scale factor = 2
Original side: 4 cm
New side: 4 × 2 = 8 cm
Reduction
Scale factor = 0.5
Original side: 10 cm
New side: 10 × 0.5 = 5 cm
Scale Factor for Area and Volume

Scale factor affects area and volume differently than length. Here's how:
Area Scale Factor:
When you scale a shape, the area changes by the square of the scale factor.
Area Scale Factor Formula
Volume Scale Factor:
For 3D objects, volume changes by the cube of the scale factor.
Volume Scale Factor Formula
Real-World Examples
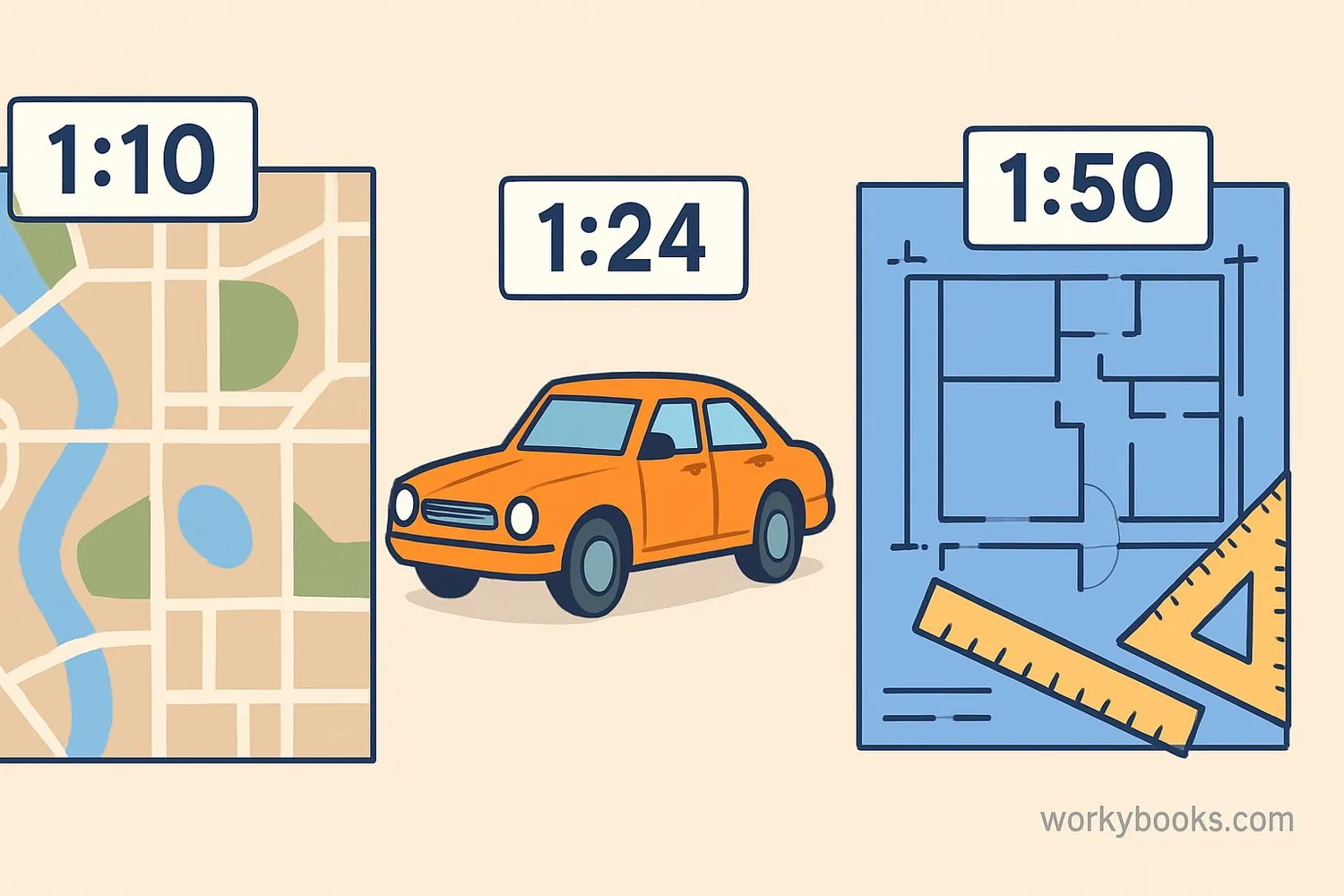
Scale factor is all around us! Here are some real-world examples:
Maps
A map might have a scale of 1:50,000. This means 1 cm on the map represents 50,000 cm (500 m) in real life. Scale factor = 1/50,000.
Model Cars
A model car that is 1/24 the size of a real car has a scale factor of 1/24. Every measurement on the model is 24 times smaller.
Blueprints
Architects use scale factors when drawing blueprints. A scale of 1:100 means 1 cm on the drawing equals 100 cm (1 m) in the actual building.
Scale Factor Quiz
Test your knowledge with this 5-question quiz. Choose the best answer for each question.
Frequently Asked Questions
Here are answers to common questions about scale factors:
Math Trivia
Discover interesting facts about scale factors and measurements:
Ancient Scaling
The ancient Egyptians used scale factors when building pyramids. Architects created small models first, then scaled up the measurements to build the massive structures.
Nature's Scaling
In nature, scale factors help explain why small animals can jump higher relative to their size than large animals. A flea can jump 200 times its body length!
Movie Magic
In movies, scale factors are used to create miniatures. A 1:24 scale model of a building filmed close-up looks like a real building on screen!
Solar System Model
If the Sun were a basketball (diameter 24 cm), Earth would be a tiny bead 2mm across, located 26 meters away! That's a scale factor of about 1:5.8 billion.





