Scalene Triangle - Definition, Examples, Quiz, FAQ, Trivia
Learn about this unique triangle with all sides of different lengths
What is a Scalene Triangle?
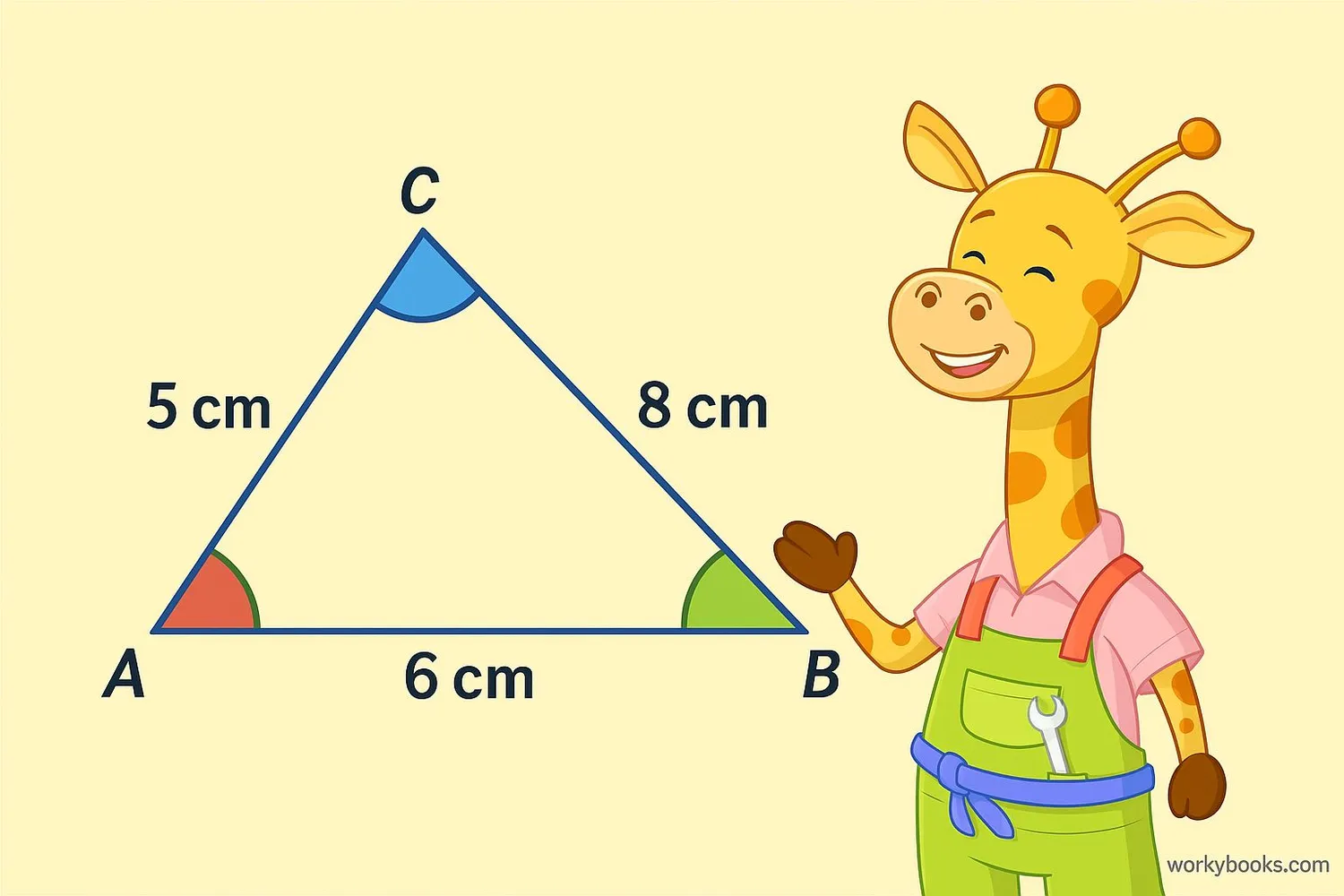
A scalene triangle is a special type of triangle where all three sides have different lengths. This also means all three angles are different sizes!
Think of it like a triangle that doesn't follow any symmetry rules. It's unique because:
- No sides are the same length
- No angles are the same size
- It has no lines of symmetry
Scalene triangles are the most common type of triangle you'll see in the real world. Look around - most triangular shapes you see are probably scalene!
Key Concept
All three sides of a scalene triangle have different lengths, and all three angles are different sizes.
Properties of Scalene Triangles
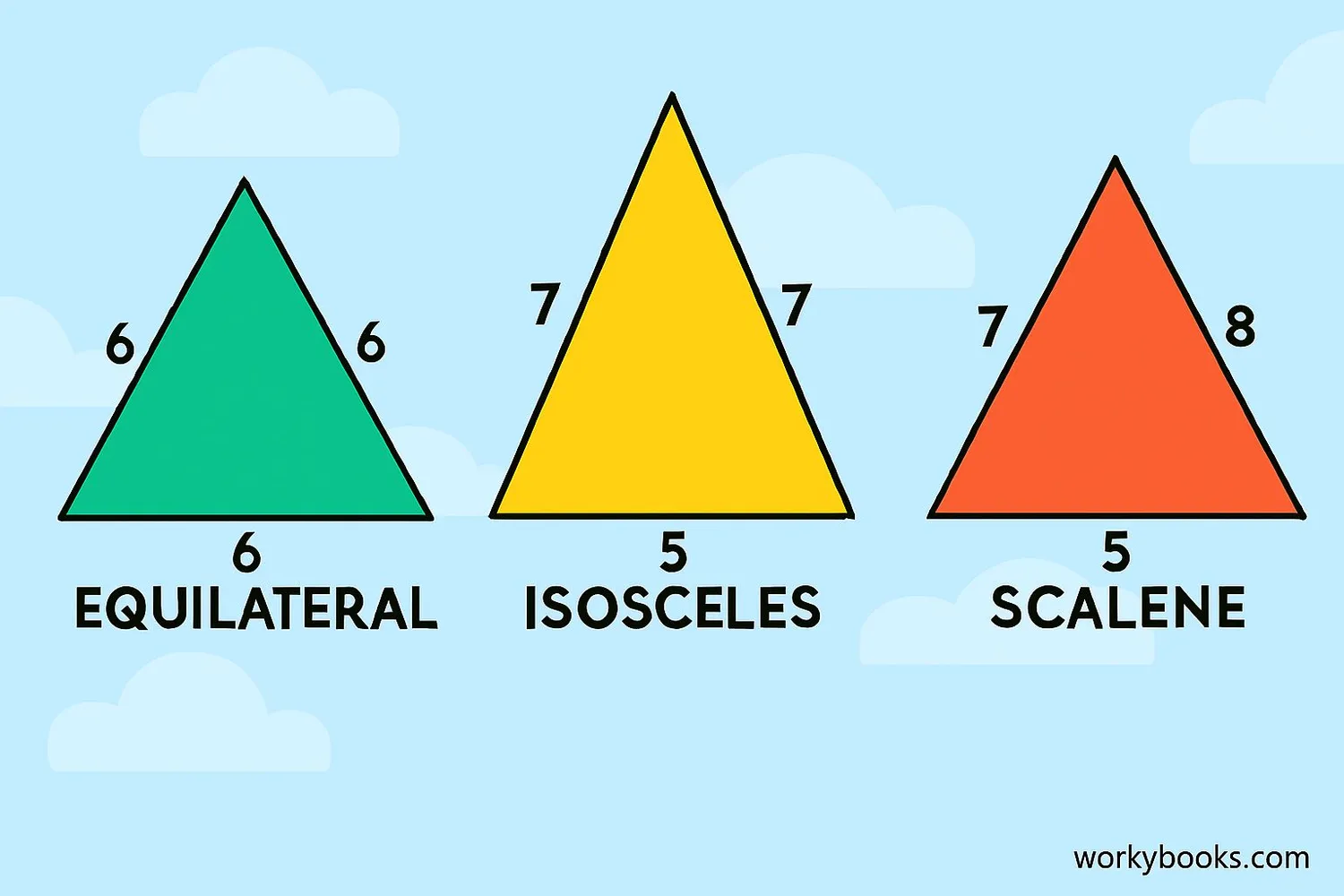
Scalene triangles have special features that make them different from other triangles:
- All sides different: No two sides have the same length
- All angles different: Each angle is a different size
- No symmetry: Scalene triangles don't have any lines of symmetry
- Unequal angles: The angles are all different, but they always add up to 180°
- Varied heights: The height from each vertex to the opposite side is different
Comparing Triangle Types
| Property | Scalene | Isosceles | Equilateral |
|---|---|---|---|
| Sides | All different | Two equal | All equal |
| Angles | All different | Two equal | All equal (60° each) |
| Symmetry | None | One line | Three lines |
| Common examples | Roof trusses, sailboat sails | Pizza slices, traffic cones | Yield signs, tortilla chips |
Remember
A triangle can't have all equal angles unless all sides are equal too. That's why scalene triangles always have all different angles.
Area of a Scalene Triangle
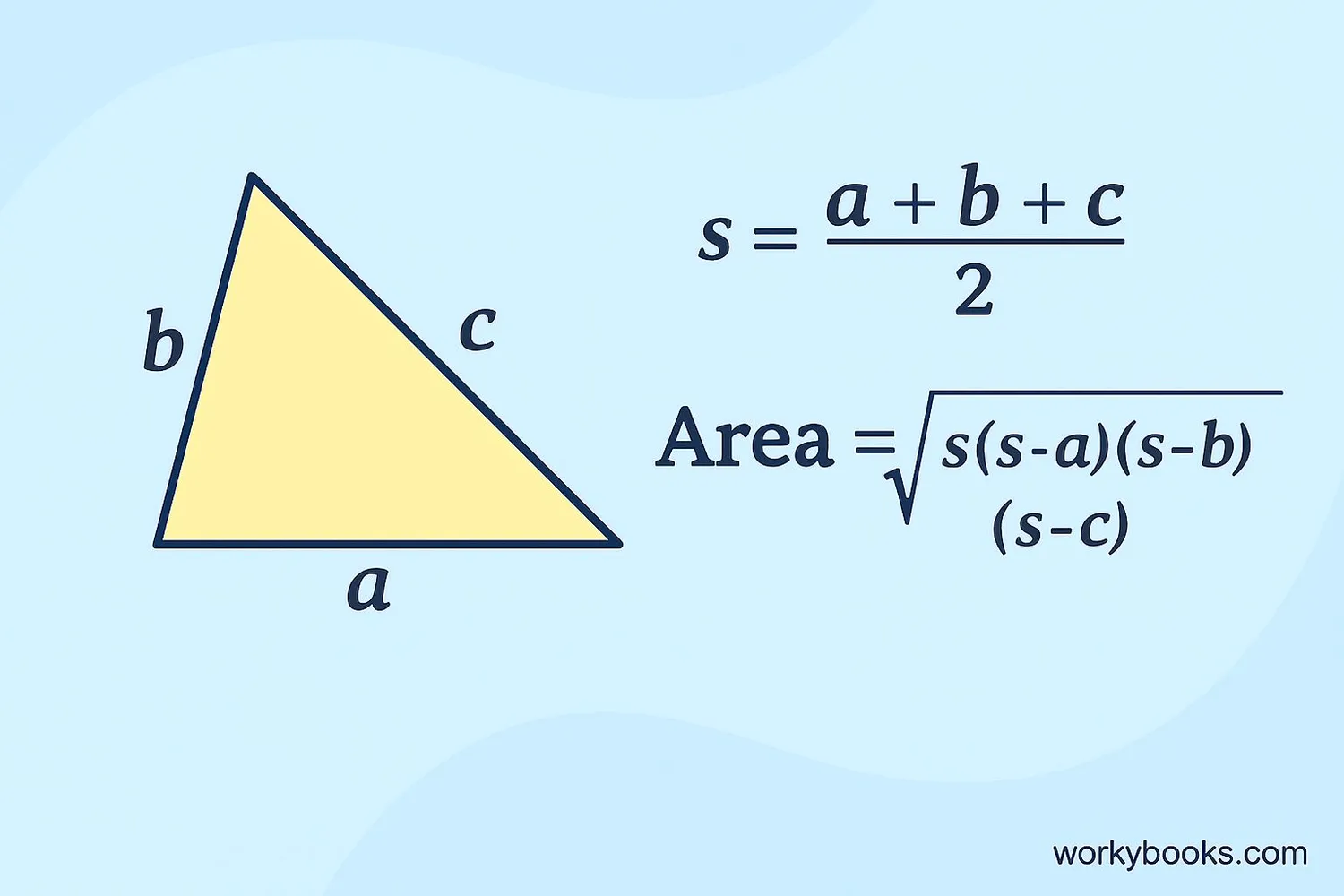
Since all sides are different, we often use Heron's formula to calculate the area of a scalene triangle. Here's how it works:
Heron's Formula
Where s = (a+b+c)/2 (semi-perimeter)
a, b, c are the lengths of the three sides
Example: Find the area of a scalene triangle with sides 5cm, 6cm, and 7cm
Step 1: Calculate s = (5+6+7)/2 = 9
Step 2: Area = √[9(9-5)(9-6)(9-7)] = √[9×4×3×2] = √[216] ≈ 14.7 cm²
Alternative Method
You can also calculate area using (base × height)/2 if you know the height corresponding to any base.
Perimeter of a Scalene Triangle
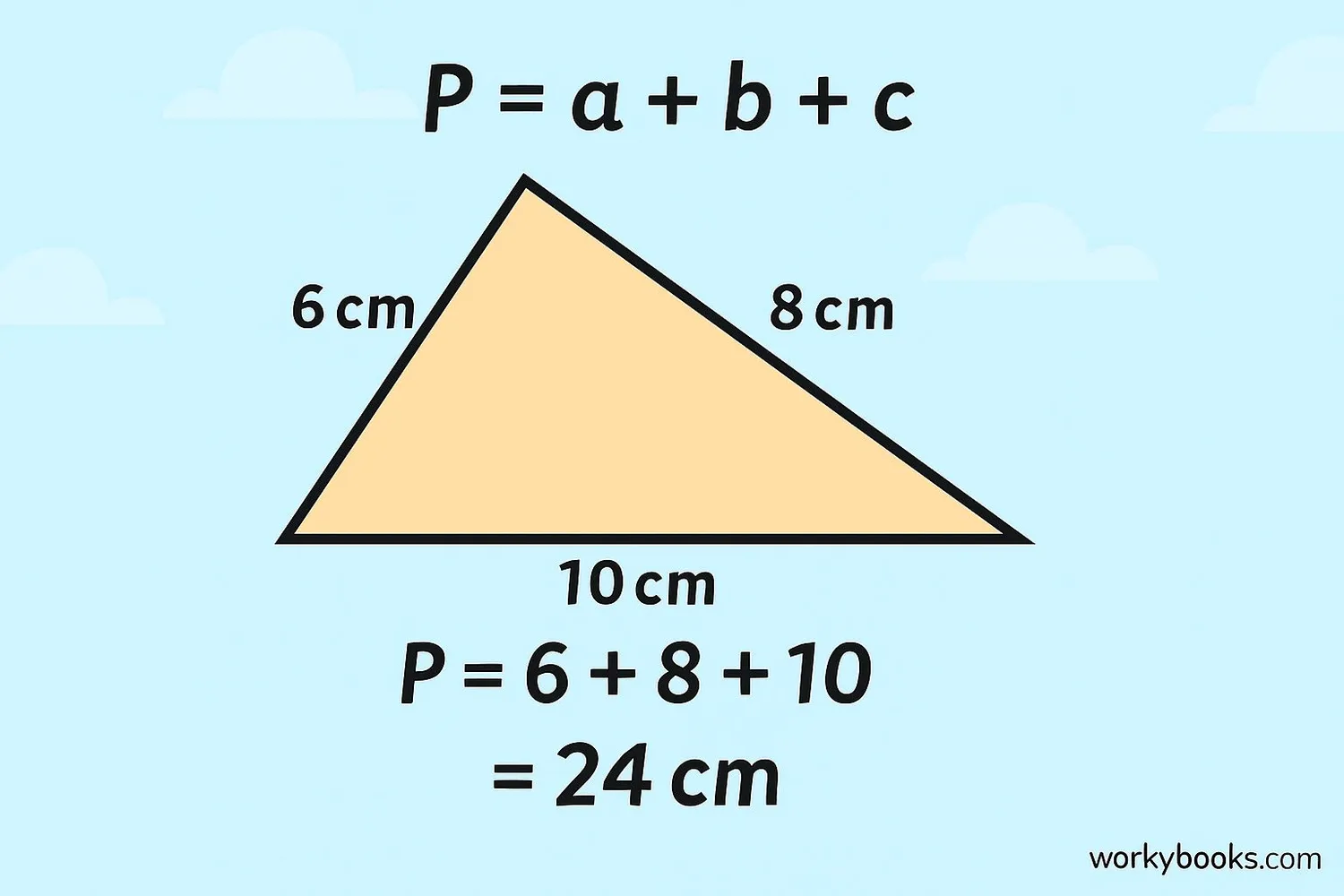
The perimeter of any triangle is simply the sum of its three sides. For scalene triangles, since all sides are different, we add all three lengths:
Perimeter Formula
Where a, b, c are the lengths of the three sides
Solution: 8 + 15 + 17 = 40cm
Perimeter Tip
The perimeter is the total distance you would walk if you went all the way around the triangle.
Real-World Examples
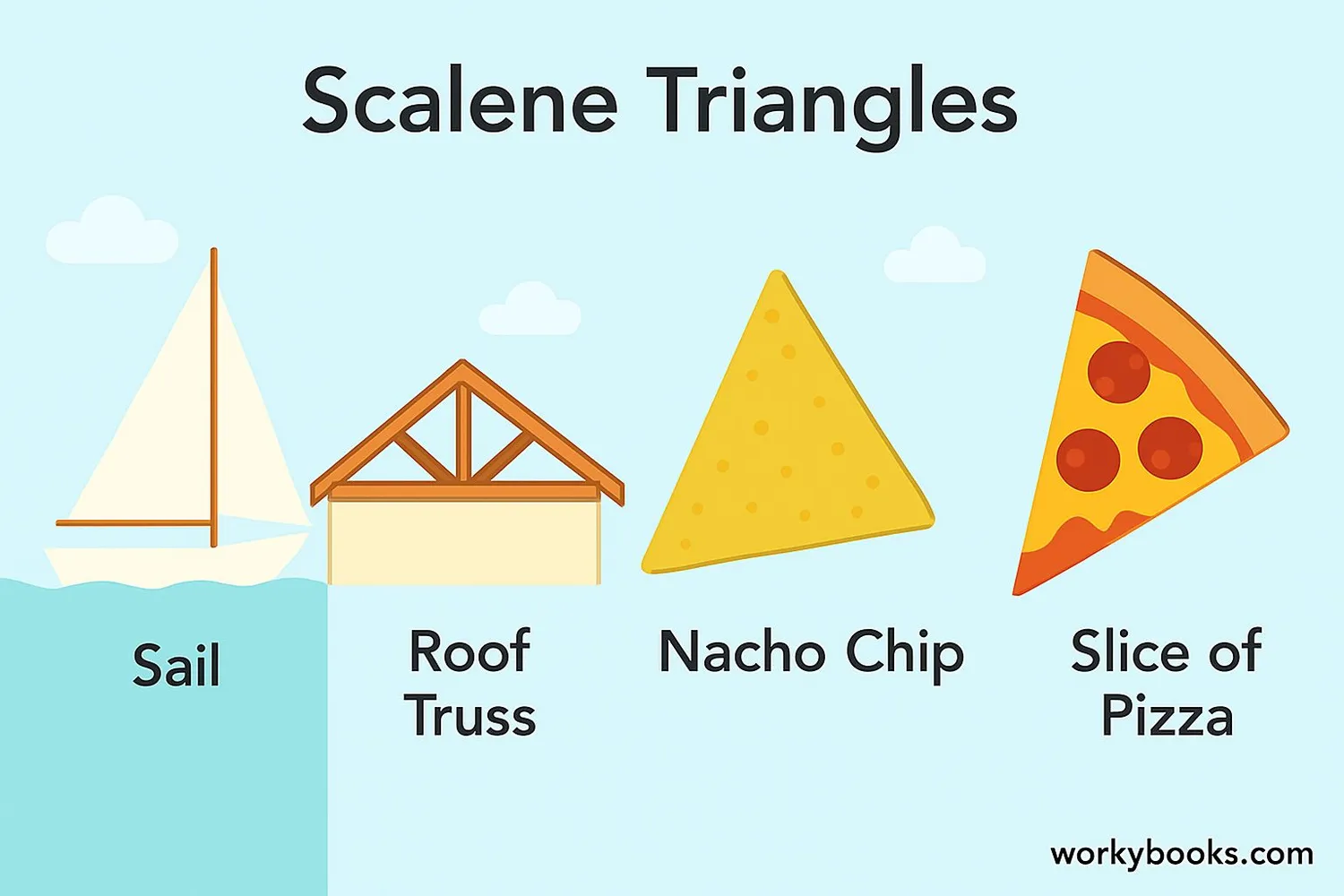
Scalene triangles are all around us! Here are some real-world examples:
Example 1: Roof trusses - Most house roofs use scalene triangles in their framework
Example 2: Sailboat sails - Triangular sails are usually scalene to catch the wind efficiently
Example 3: Nacho chips - Most tortilla chips are irregular scalene triangles
Example 4: Pizza slices - When pizza is cut unevenly, the slices become scalene triangles
Look Around
Can you find any scalene triangles in your classroom or home? Look at objects like bookshelves, desks, or wall decorations.
Triangle Practice Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about scalene triangles:
Triangle Trivia
Discover interesting facts about triangles:
Ancient Geometry
The ancient Egyptians used triangles in their pyramid constructions over 4,500 years ago. The Great Pyramid of Giza incorporates many triangular shapes in its structure.
Strongest Shape
Triangles are the strongest geometric shape because they distribute weight evenly. That's why you see triangles in bridges, roofs, and towers - they provide great strength!
Space Triangles
Astronomers use triangles to measure distances in space! By measuring angles between stars from different positions, they can calculate vast distances in our universe.
Largest Triangle
The largest man-made triangle is the triangular Bermuda Island in the Atlantic Ocean. It spans about 500,000 square miles between Miami, Bermuda, and Puerto Rico.





