Slope - Definition, Examples, Quiz, FAQ, Trivia
Learn about slope with visual examples, real-world applications, and practice activities
What is Slope?
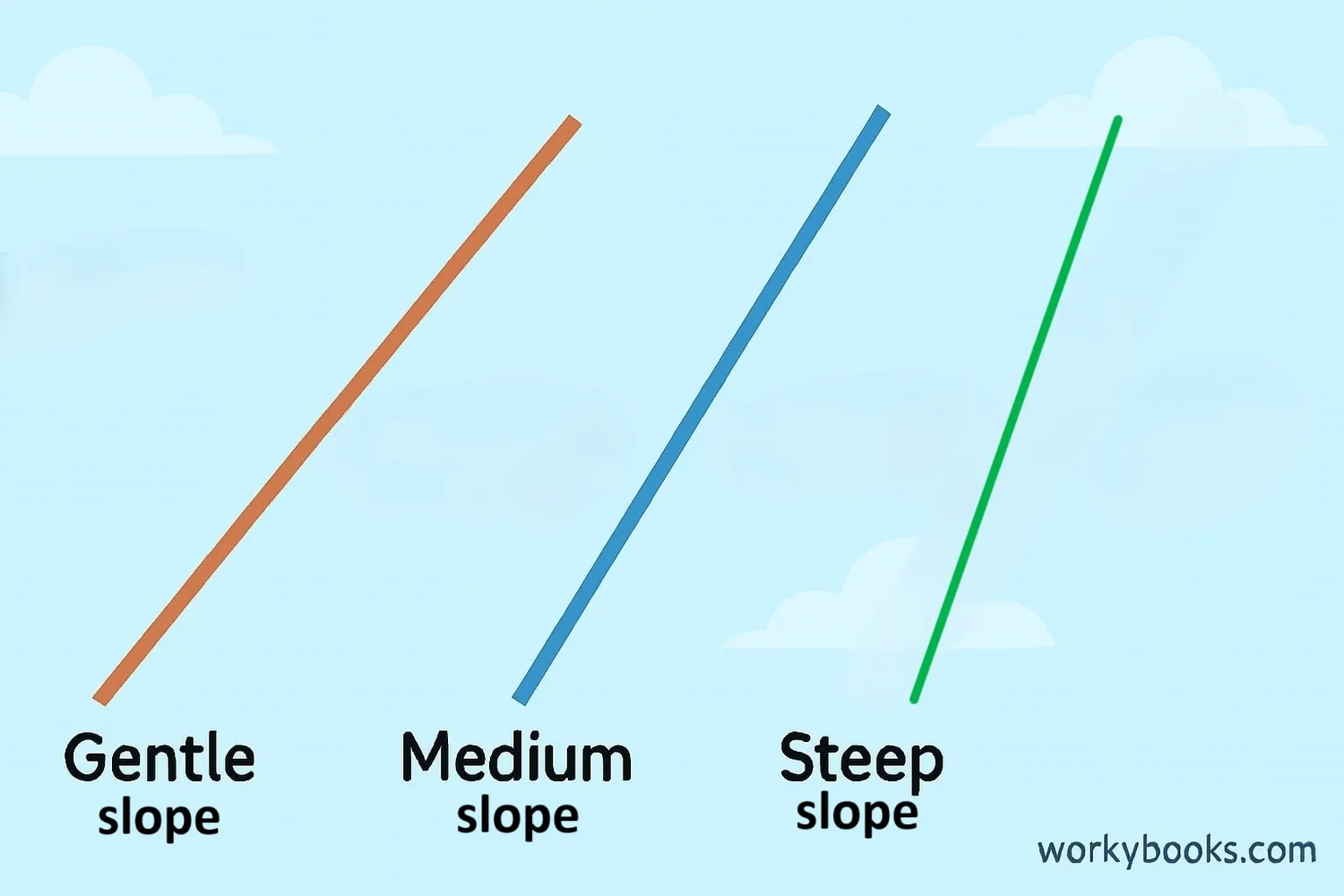
Slope is a measure of how steep a line is. It tells us how much a line rises or falls as we move along it.
Think of slope like a hill: a steep hill has a large slope, while a gentle hill has a small slope. In math, slope is represented by the letter m.
Slope is calculated by dividing the vertical change (rise) by the horizontal change (run) between any two points on a line:
Slope (m) = Rise ÷ Run
Slope helps us understand how quickly things change. For example, a steep slope on a graph might show that something is changing quickly over time.
Key Concept
Slope measures steepness: higher slope values mean steeper lines, while lower values mean flatter lines.
How to Calculate Slope
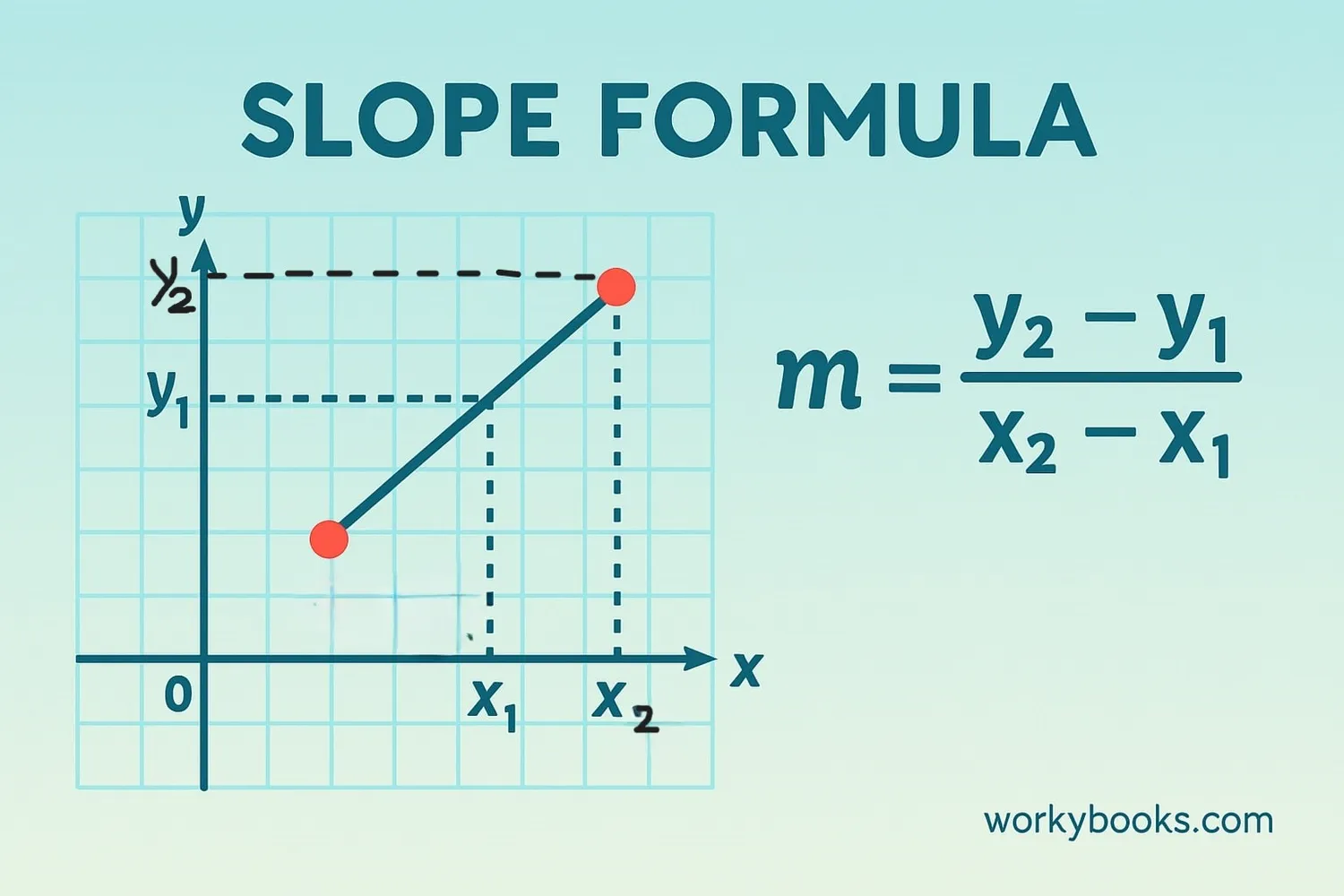
There are two main ways to calculate slope:
1. Rise over Run:
Find how much the line rises (changes vertically) and how much it runs (changes horizontally) between two points.
Slope Formula
Rise is the vertical change, run is the horizontal change
If you know two points on a line: (x₁, y₁) and (x₂, y₂)
Coordinate Formula
Subtract the y-values and divide by the difference of x-values
Step 1: Identify points: x₁=1, y₁=2, x₂=4, y₂=6
Step 2: Calculate rise: 6 - 2 = 4
Step 3: Calculate run: 4 - 1 = 3
Step 4: Slope = 4 ÷ 3 ≈ 1.33
Remember
Slope is constant for a straight line - you'll get the same value no matter which two points you choose!
Types of Slope
Positive Slope
Line rises from left to right
Example: m = 2, m = 0.5
Negative Slope
Line falls from left to right
Example: m = -1, m = -0.3
Zero Slope
Horizontal line, no rise
Example: m = 0
Undefined Slope
Vertical line, no run
Example: m = undefined
Lines can have different types of slopes:
Positive Slope: The line rises as you move from left to right. This means for every step right, you also go up.
Negative Slope: The line falls as you move from left to right. This means for every step right, you go down.
Zero Slope: The line is perfectly horizontal. There's no rise, only run. The slope is 0.
Undefined Slope: The line is perfectly vertical. There's no run, only rise. We say the slope is undefined because you can't divide by zero.
Slope Tip
Remember slope types with this phrase: "Positive slopes rise, negative slopes fall, zero is flat, undefined stands tall!"
Slope-Intercept Form
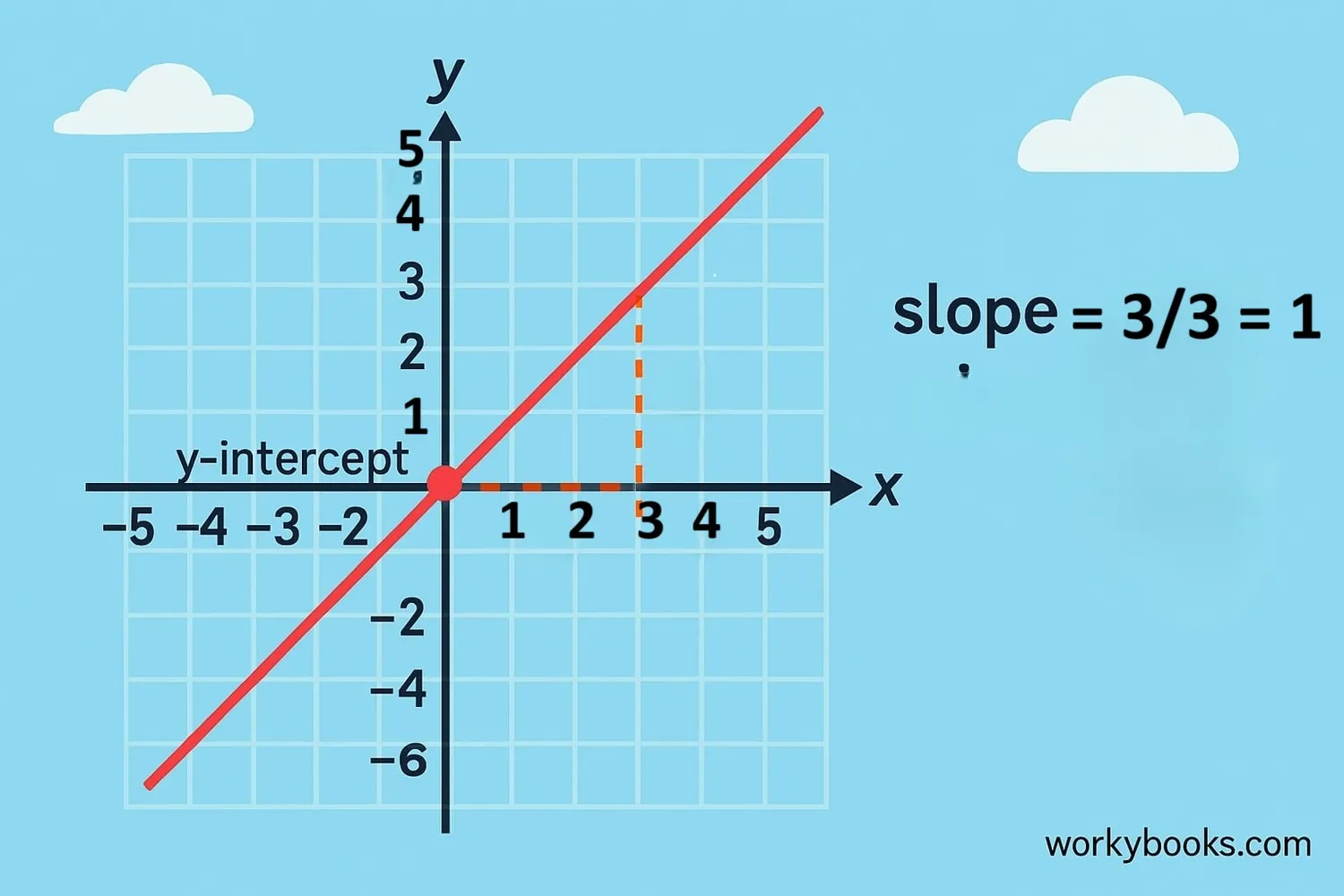
The slope-intercept form is a special way to write the equation of a line:
Slope-Intercept Form
Where m is the slope and b is the y-intercept
• m tells us the slope (steepness) of the line
• b tells us where the line crosses the y-axis
Example: In the equation y = 2x + 3
• The slope (m) is 2, meaning for every 1 unit right, we go 2 units up
• The y-intercept (b) is 3, meaning the line crosses the y-axis at (0, 3)
This form makes it easy to graph a line and understand its properties!
Remember
In y = mx + b, the y-intercept is always the point (0, b) on the graph.
Real-World Examples
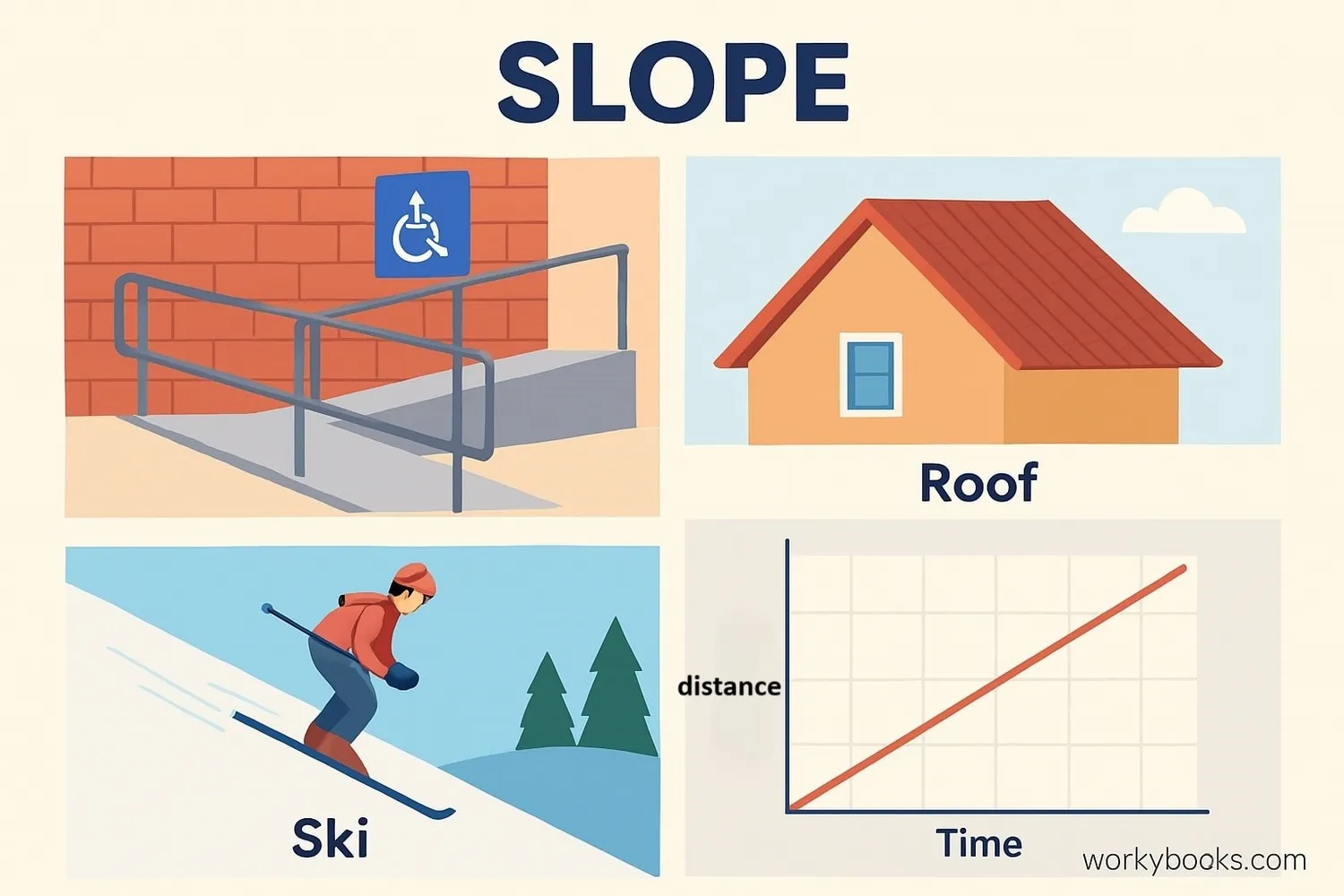
Slope isn't just for math class - we see it everywhere in real life!
Example 1: Wheelchair Ramps
Ramps have slope to make them accessible. A gentle slope (small m) is easier to use than a steep slope.
Example 2: Roofs
The pitch of a roof is its slope. Steeper roofs shed snow and rain better.
Example 3: Hiking Trails
Trail difficulty depends on slope. Gentle slopes are easy, steep slopes are challenging.
Example 4: Speed Graphs
In science, slope on a distance-time graph shows speed. Steeper slope = faster speed.
Example 5: Business
A company's profit graph might show increasing profit (positive slope) or decreasing profit (negative slope).
Real-World Tip
Look for slope around you - in stairs, slides, or even the angle of sunlight!
Slope Practice Quiz
Test your slope knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about slope:
Math Trivia
Discover interesting facts about slope:
Ancient Slope
The concept of slope dates back to ancient Egypt, where builders used slope calculations to construct pyramids with precise angles.
Steepest Road
Baldwin Street in New Zealand has a slope of about 35% - that's a rise of 35 meters for every 100 meters horizontal!
Space Exploration
NASA engineers calculate precise slopes for rocket launch trajectories to ensure spacecraft enter orbit correctly.
Ski Slopes
Ski slopes are rated by their steepness: green circles (gentle), blue squares (medium), black diamonds (steep), and double black (very steep).





