Slope-Intercept Form - Definition, Examples, Quiz, FAQ, Trivia
Learn to graph linear equations with y=mx+b using easy explanations and practice activities
What is Slope-Intercept Form?
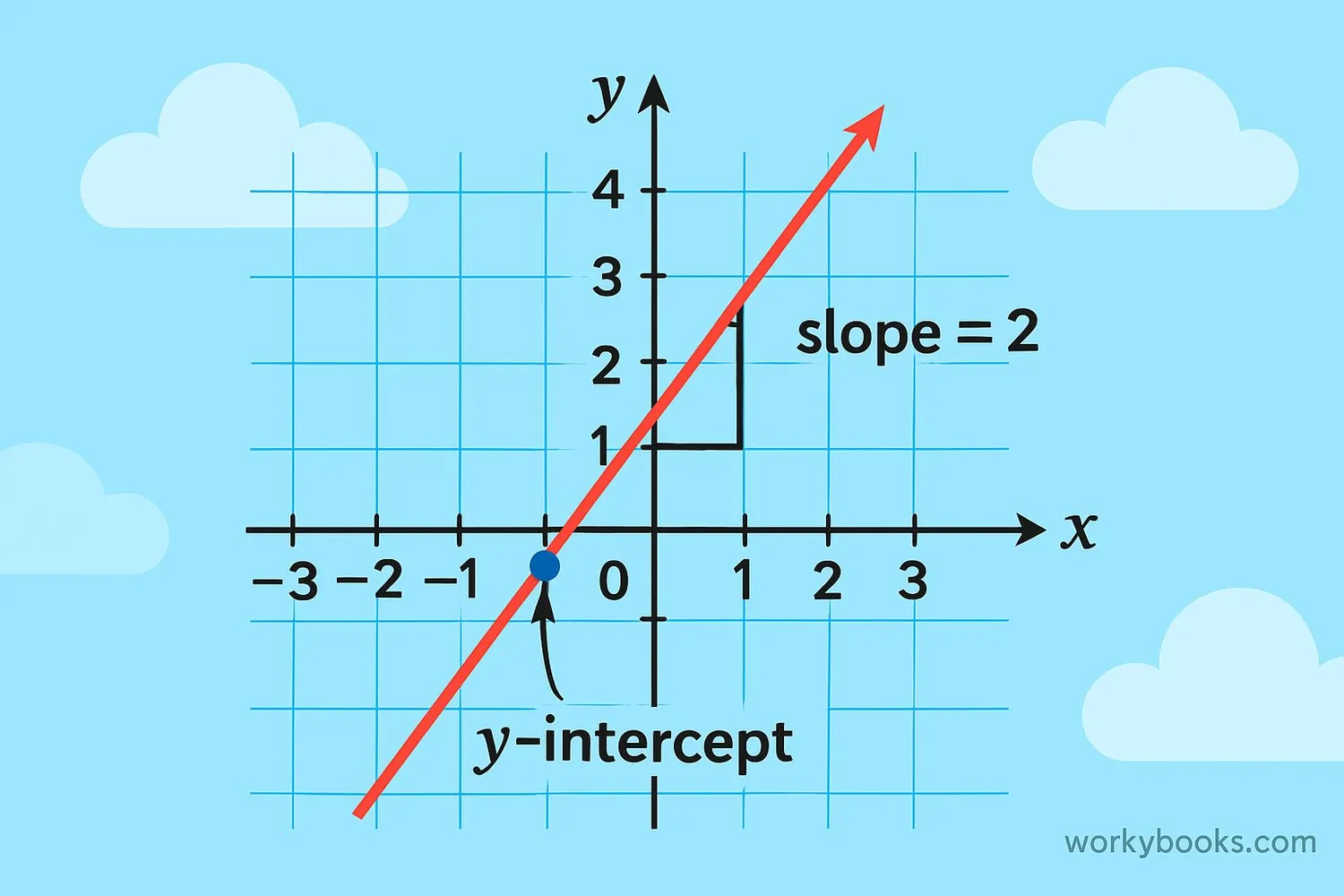
The slope-intercept form is a special way to write the equation of a straight line. It makes graphing lines easy because it shows two important pieces of information:
1. The slope (m) - How steep the line is
2. The y-intercept (b) - Where the line crosses the y-axis
The slope-intercept form is written as:
Slope-Intercept Formula
• y is the y-coordinate
• x is the x-coordinate
• m is the slope of the line
• b is the y-intercept
Key Concept
Every straight line can be written in slope-intercept form (y=mx+b). This form is especially helpful for graphing because it shows exactly where the line starts on the y-axis and how it slopes.
Understanding y = mx + b
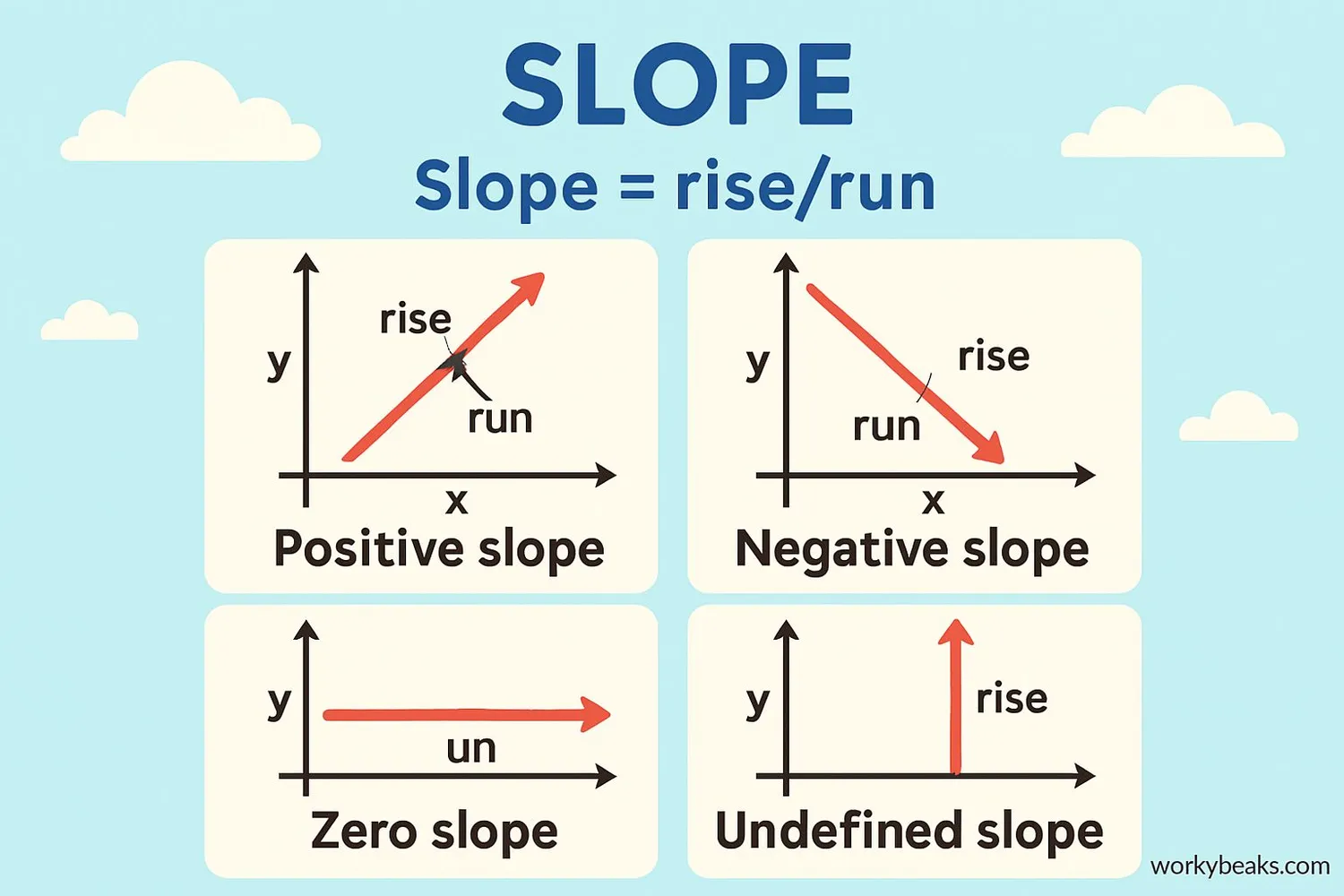
Let's break down the equation y = mx + b to understand what each part means:
The Slope (m):
The slope tells us how steep the line is and in which direction it goes:
- Positive slope (m > 0): The line rises as it moves from left to right
- Negative slope (m < 0): The line falls as it moves from left to right
- Zero slope (m = 0): The line is horizontal
- Undefined slope: The line is vertical (but this can't be written in slope-intercept form)
The Y-Intercept (b):
This is the point where the line crosses the y-axis. It's always at the point (0, b). For example:
- If b = 3, the line crosses the y-axis at (0, 3)
- If b = -2, the line crosses the y-axis at (0, -2)
Slope Calculation
Rise = Change in y-values
Run = Change in x-values
Remember
The slope (m) is a ratio that tells us how much the line rises (or falls) for each step we take to the right. For a slope of 2, the line goes up 2 units for every 1 unit it moves to the right.
Graphing Linear Equations
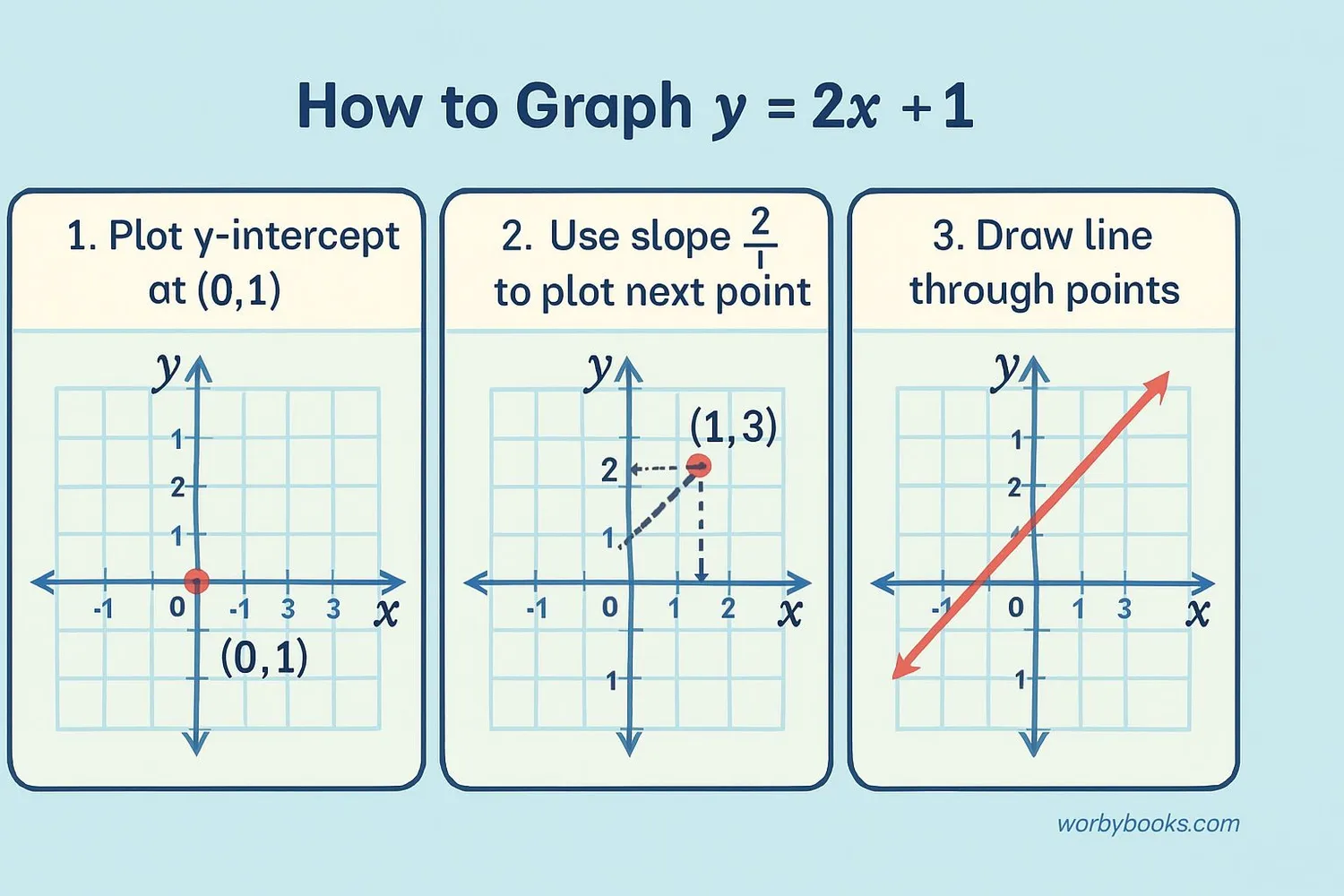
Graphing linear equations in slope-intercept form is easy when you follow these steps:
Step 1: Start by plotting the y-intercept (b) on the y-axis.
Step 2: Use the slope (m) to find another point. Remember, slope is rise over run.
Step 3: Draw a straight line through the two points.
Example: Graph the equation y = 2x + 1
• Step 1: Plot the y-intercept: (0, 1)
• Step 2: Slope is 2, which means rise=2, run=1. From (0,1), move up 2 units and right 1 unit to (1,3)
• Step 3: Draw a line through (0,1) and (1,3)
Graphing Tip
Always start with the y-intercept (b) when graphing. Then use the slope to find at least one more point. The more points you plot, the more accurate your line will be!
Converting to Slope-Intercept Form
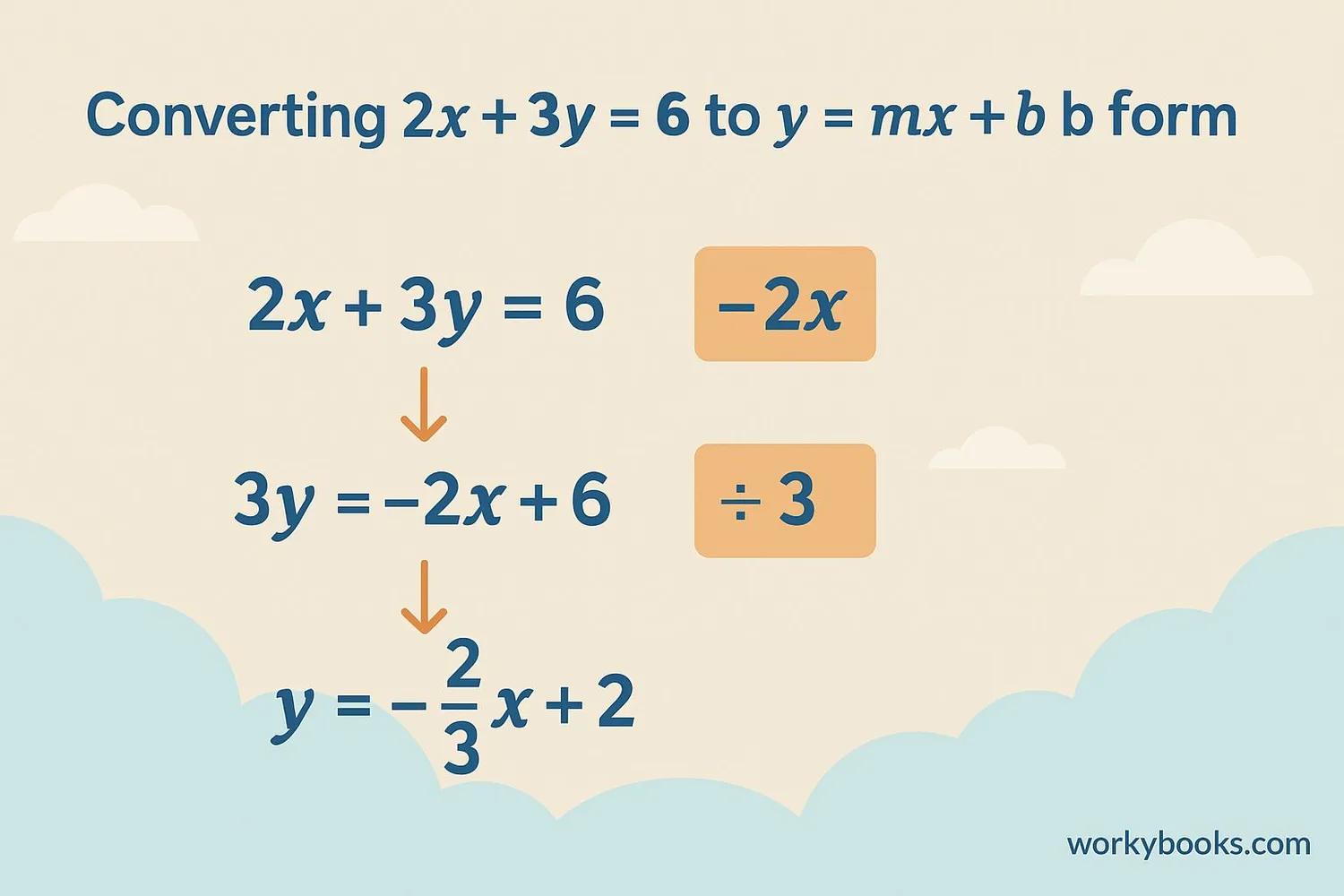
Sometimes equations are not written in slope-intercept form. Here's how to convert them:
From Standard Form (Ax + By = C):
- Move the x-term to the other side: By = -Ax + C
- Divide every term by B: y = (-A/B)x + (C/B)
- Now it's in y = mx + b form with m = -A/B and b = C/B
Example: Convert 2x + 3y = 6 to slope-intercept form
• Step 1: 3y = -2x + 6
• Step 2: y = (-2/3)x + 2
From Point-Slope Form (y - y₁ = m(x - x₁)):
- Distribute the slope: y - y₁ = mx - mx₁
- Add y₁ to both sides: y = mx - mx₁ + y₁
- Now it's in y = mx + b form with b = -mx₁ + y₁
Example: Convert y - 3 = 4(x - 2) to slope-intercept form
• Step 1: y - 3 = 4x - 8
• Step 2: y = 4x - 8 + 3
• Step 3: y = 4x - 5
Conversion Tip
When converting to slope-intercept form, remember the goal is to get "y" by itself on the left side of the equation. Use inverse operations to isolate y.
Slope-Intercept Form Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about slope-intercept form:
Math Trivia
Discover interesting facts about linear equations and algebra:
Ancient Origins
The concept of linear equations dates back to ancient Egypt and Babylon around 1800 BC. The Rhind Mathematical Papyrus contains problems that we now recognize as linear equations.
Real-World Applications
Slope-intercept form is used in countless real-world applications: calculating speed (distance vs. time), predicting costs (fixed cost + variable cost), and even in video game programming for character movement.
Space Exploration
NASA engineers use linear equations to calculate rocket trajectories. The slope-intercept form helps them determine how much fuel is needed based on distance and weight, ensuring accurate space missions.
Mathematical Record
The longest straight-line path you can sail on Earth without hitting land is approximately 32,000 km. This path can be modeled using linear equations with an extremely small slope value.





