Square Root of 18 - Definition, Examples, Quiz, FAQ, Trivia
Learn what square roots are, how to calculate them, and why √18 is special
What is Square Root?
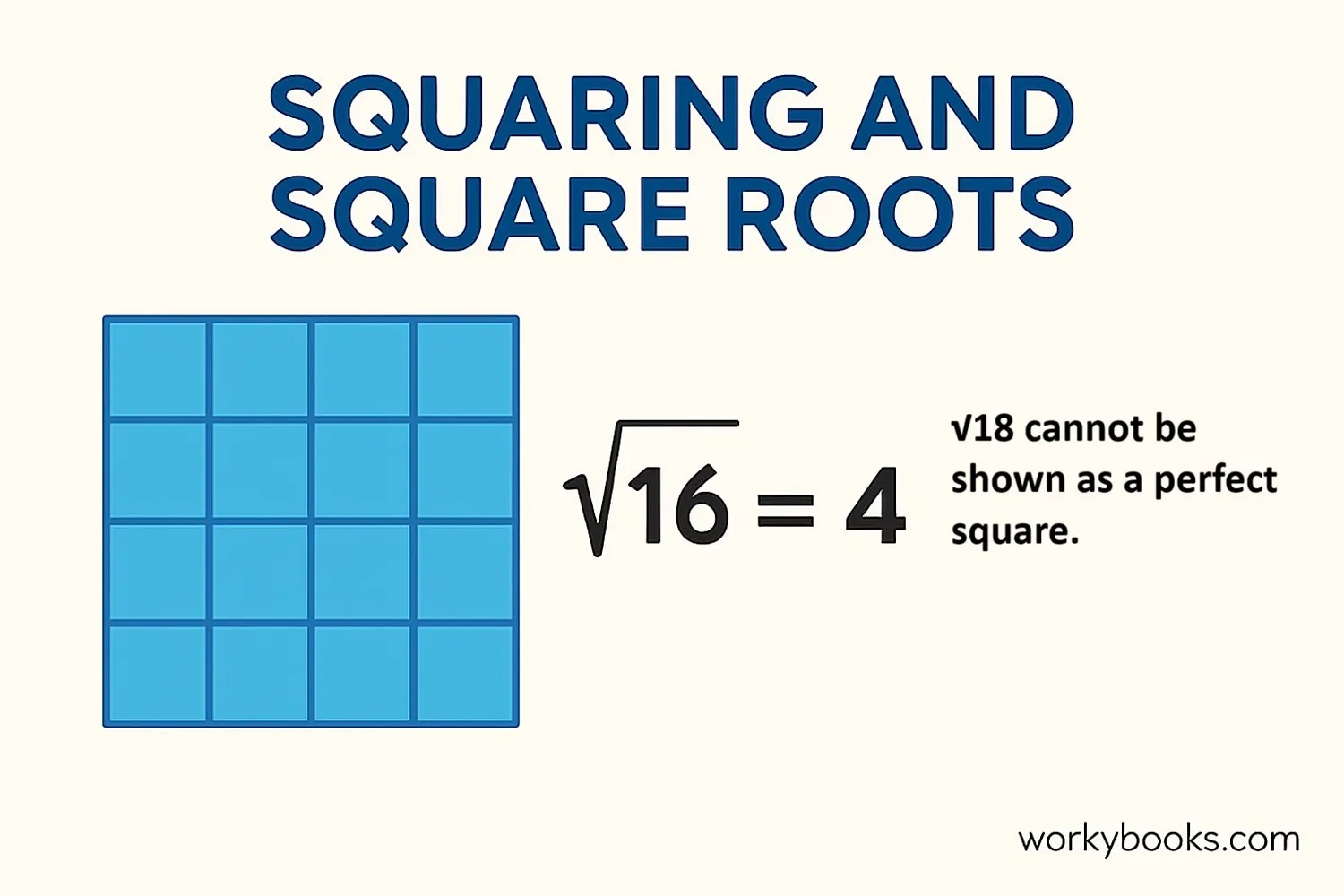
A square root is a special number that, when multiplied by itself, gives the original number.
For example, the square root of 9 is 3 because 3 × 3 = 9.
We write square roots using the radical symbol: √number.
The number inside the radical symbol is called the radicand.
For √18, 18 is the radicand.
Numbers like 1, 4, 9, 16, and 25 are called perfect squares because their square roots are whole numbers.
The number 18 is not a perfect square because its square root isn't a whole number.
Key Concept
The square root of 18 is approximately 4.2426. This means 4.2426 × 4.2426 ≈ 18.
Perfect Squares Chart
Calculating √18
Since 18 isn't a perfect square, we need special methods to find its square root. Here are two ways to calculate √18:
Method 1: Prime Factorization
1 Factor 18 into prime numbers: 18 = 2 × 3 × 3
2 Group the prime factors into pairs: 18 = 2 × (3 × 3)
3 For each pair, take one number out of the square root: √18 = √(3² × 2) = 3√2
4 Calculate the value: 3 × √2 ≈ 3 × 1.4142 = 4.2426
Method 2: Long Division
1 Start by placing a bar over 18.00 00 00
2 Find the largest number whose square is ≤ 18 (which is 4)
3 Subtract 16 (4×4) from 18, bring down two zeros → 200
4 Double the quotient (4×2=8). Find digit (d) such that (80+d)×d ≤ 200 (d=2)
5 Continue the process to get more decimal places: √18 ≈ 4.2426
Simplified Radical Form
This is the simplest radical form of the square root of 18.
Rational or Irrational?
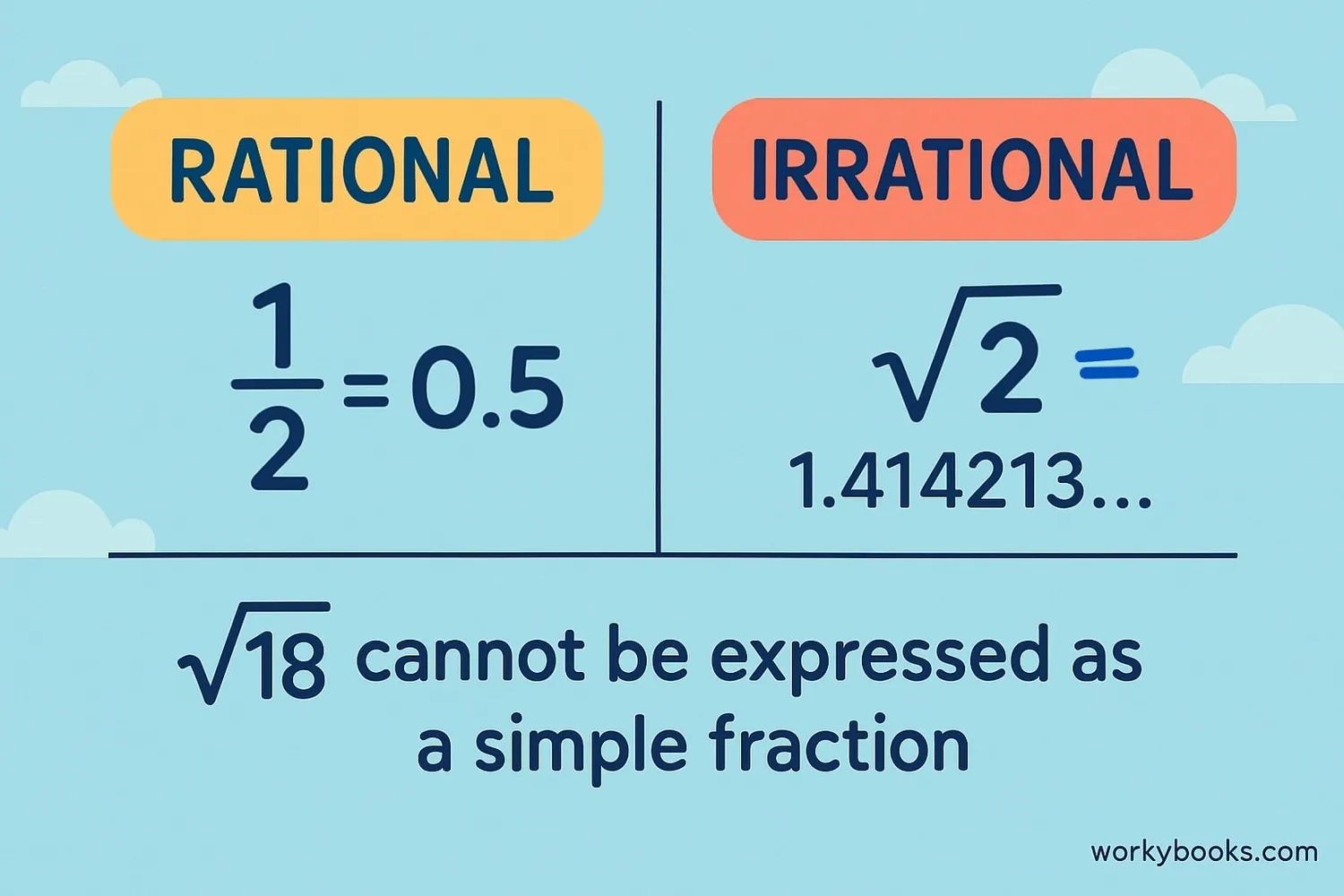
Numbers can be either rational or irrational:
Rational numbers can be written as a fraction (like 1/2 or 0.75).
Their decimals either end or repeat a pattern.
Irrational numbers cannot be written as a simple fraction.
Their decimals go on forever without repeating.
Since 18 is not a perfect square, √18 is an irrational number.
Its decimal goes on forever without repeating: 4.242640687...
Why? Because √18 = √(9×2) = 3√2, and √2 is irrational.
When you multiply a rational number (3) by an irrational number (√2), the result is irrational.
Remember
The square root of any number that isn't a perfect square is irrational.
| Number | Perfect Square? | Square Root | Rational or Irrational? |
|---|---|---|---|
| 16 | Yes | 4 | Rational |
| 18 | No | ≈4.2426 | Irrational |
| 25 | Yes | 5 | Rational |
| 2 | No | ≈1.4142 | Irrational |
Practice Quiz
Test your understanding of square roots with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about square roots and √18:
Math Trivia
Discover interesting facts about square roots and mathematics:
Ancient Square Roots
The Babylonians had methods for approximating square roots as early as 2000 BCE! They used a method similar to our modern long division method.
Irrational Discovery
The ancient Greeks discovered irrational numbers when studying the diagonal of a square. They found that √2 couldn't be expressed as a ratio of two integers, which surprised many mathematicians!
Radical Symbol Origin
The radical symbol (√) was first used in 1525 by mathematician Christoph Rudolff. It may have evolved from the letter "r" for "radix," the Latin word for root.
Calculating Digits
Computers have calculated √2 to over 10 trillion digits! While we don't need that many digits for everyday math, it helps scientists test computer processing power.





