Evaluate - Definition, Examples, Quiz, FAQ, Trivia
Learn how to find the value of expressions with variables using substitution and simplification
What Does "Evaluate" Mean in Math?
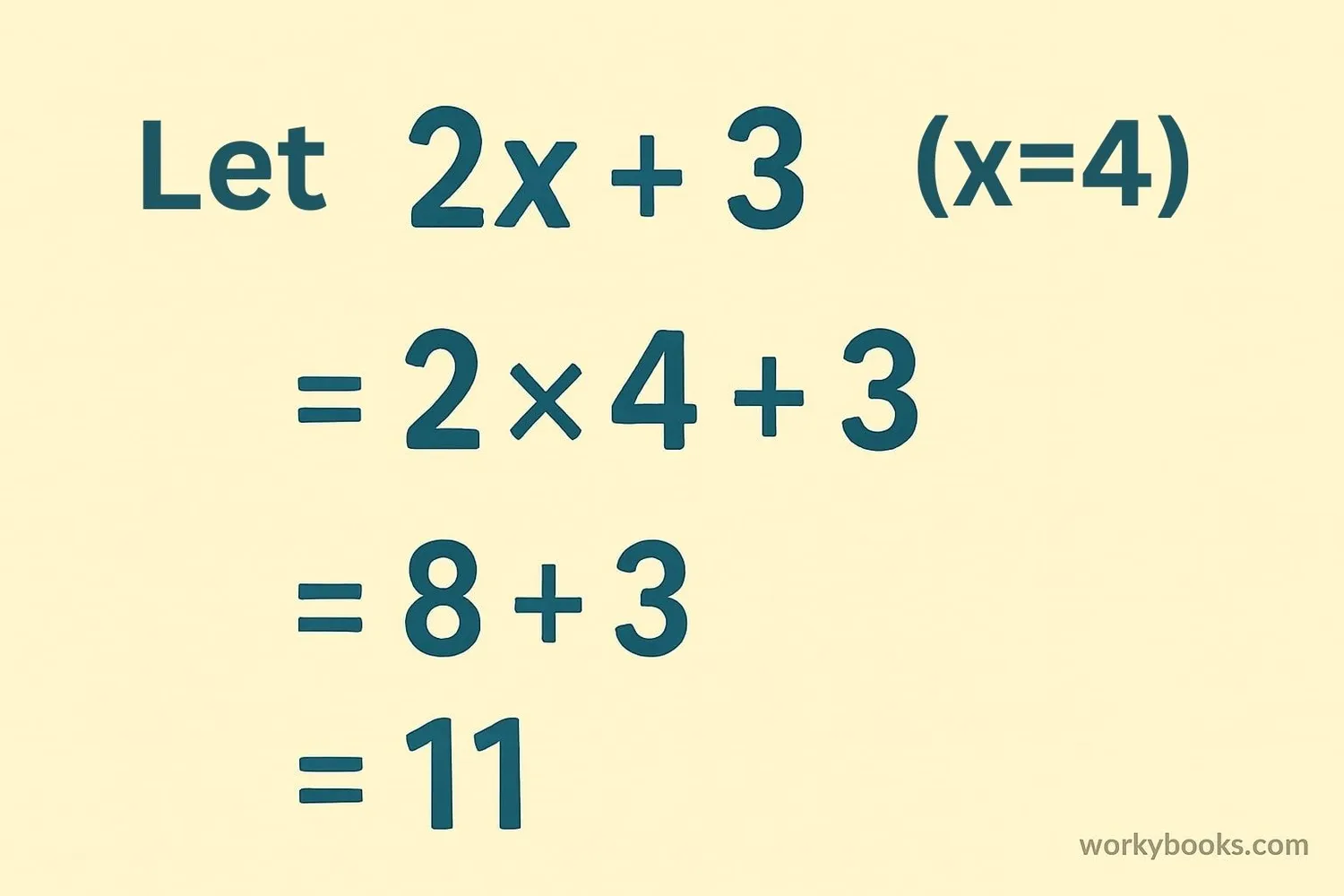
In mathematics, to evaluate means to find the value of an expression. When an expression contains variables (like x, y, or z), we substitute those variables with given numbers and then simplify the expression to find the final value.
Think of it like following a recipe: if a recipe says "2 cups of flour + 1 egg," and you know that "1 cup of flour = 120 grams," you can evaluate the expression to find the total weight: 2×120 + 1×50 = 240 + 50 = 290 grams.
Evaluating expressions helps us solve real-world problems and is a fundamental skill in algebra. It's like being a math detective who follows clues to find the final answer!
Key Concept
Evaluation means substituting variables with their values and then simplifying the expression using the correct order of operations.
How to Evaluate Expressions

Evaluating expressions follows a clear process. Let's break it down into simple steps:
Steps to Evaluate Expressions
- Identify the expression and the values of any variables.
- Substitute each variable with its given numerical value.
- Follow the order of operations (PEMDAS: Parentheses, Exponents, Multiplication/Division, Addition/Subtraction).
- Simplify step by step until you have a single value.
Remember PEMDAS
Parentheses, Exponents, Multiplication & Division (left to right), Addition & Subtraction (left to right)
Let's try a simple example: Evaluate 3x + 5 when x = 2
Step 1: Identify the expression → 3x + 5, and x = 2
Step 2: Substitute → 3(2) + 5
Step 3: Follow order of operations → Multiplication first: 3×2 = 6, then Addition: 6 + 5
Step 4: Simplify → 11
So when x = 2, the expression 3x + 5 evaluates to 11.
Remember
Always use parentheses when substituting to avoid mistakes with negative numbers or complicated expressions.
Examples of Evaluating Expressions

Let's look at several examples of evaluating expressions with different operations:
Example Table
| Expression | Values | Substitution | Evaluation Steps | Result |
|---|---|---|---|---|
| 2x + 7 | x = 5 | 2(5) + 7 | 10 + 7 = 17 | 17 |
| y² - 3y | y = 4 | 4² - 3(4) | 16 - 12 = 4 | 4 |
| 5a + 2b | a=3, b=2 | 5(3) + 2(2) | 15 + 4 = 19 | 19 |
| (m + n) × 2 | m=7, n=3 | (7 + 3) × 2 | 10 × 2 = 20 | 20 |
| 10 - p ÷ 2 | p = 8 | 10 - 8 ÷ 2 | 10 - 4 = 6 | 6 |
Notice how in the last example, we did the division before the subtraction. That's because we follow the order of operations (PEMDAS). Division comes before subtraction.
Try creating your own examples with different values. The more you practice, the easier evaluating expressions will become!
Practice Tip
When practicing, always write out the substitution step clearly. This helps you avoid mistakes and shows your work.
Evaluation Practice Quiz
Test your evaluation skills with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about evaluating expressions:
Math Trivia
Discover interesting facts about algebra and expressions:
Ancient Algebra
The word "algebra" comes from the Arabic word "al-jabr" which means "reunion of broken parts." It was first used in a mathematical book written by Persian mathematician Al-Khwarizmi around 820 AD.
Variable Origins
The use of x, y, and z as variables in algebra became popular thanks to French mathematician René Descartes in the 17th century. Before that, mathematicians used words or abbreviations.
Math in Daily Life
We use algebraic expressions every day without realizing it! When calculating tips, determining sale prices, or converting measurements, we're essentially evaluating expressions.
Longest Equation
The longest mathematical equation ever written contains about 200 terabytes of text! It would take approximately 6.5 billion pages to write it out on paper.





