Hypotenuse Leg Theorem (HL Theorem) - Definition, Examples, Quiz, FAQ, Trivia
Learn about right triangle congruence with easy explanations, visual examples, and practice activities
What is the Hypotenuse Leg Theorem?
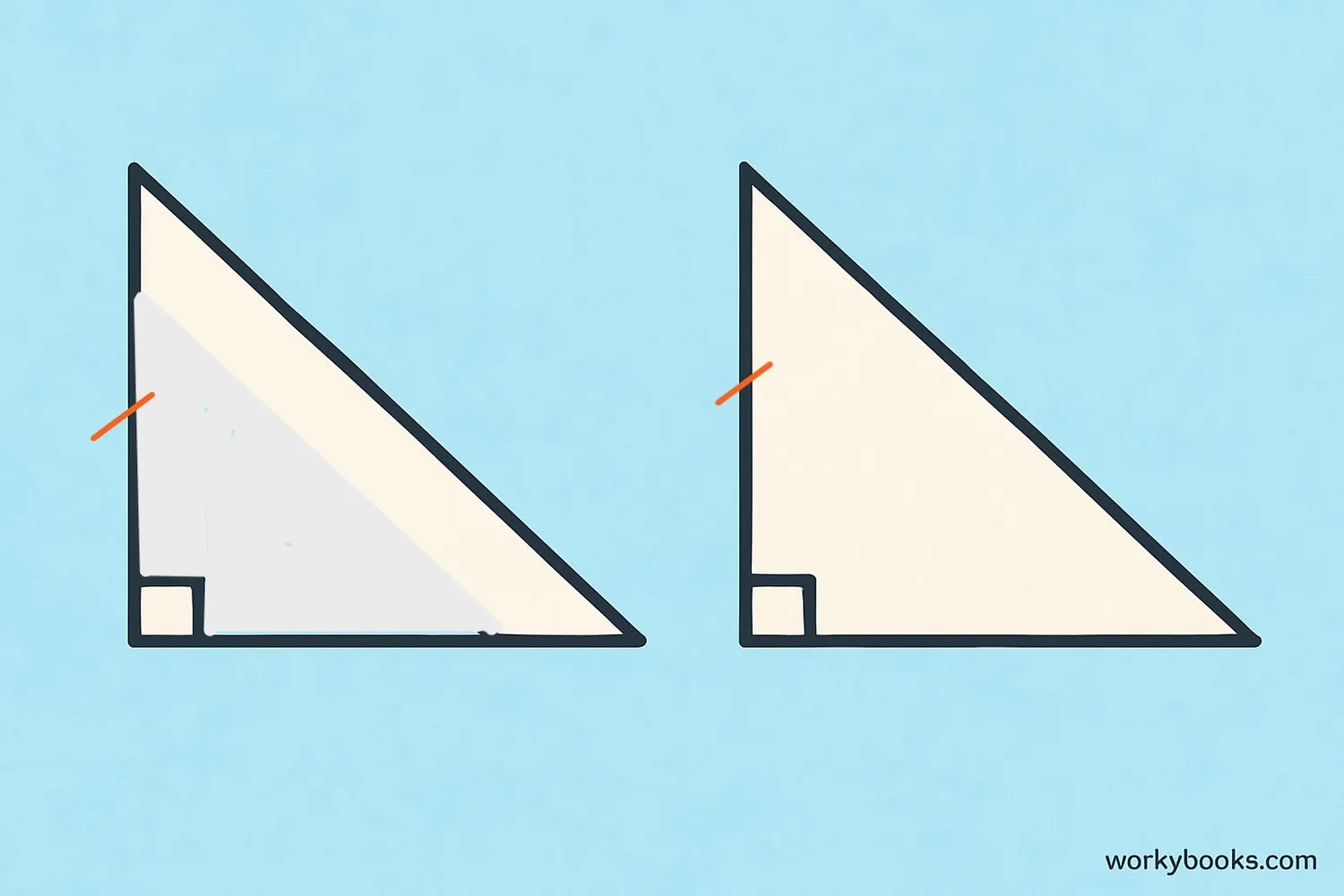
The Hypotenuse Leg Theorem (often abbreviated as HL Theorem) is a special rule that helps us determine when two right triangles are congruent. Congruent means they have exactly the same size and shape.
The theorem states that if the hypotenuse and one leg of a right triangle are equal to the hypotenuse and one leg of another right triangle, then the two triangles are congruent.
This theorem only works for right triangles because the right angle guarantees that the other two angles will also be equal when the hypotenuse and one leg are equal.
Key Concept
The HL Theorem only applies to right triangles. It's a shortcut that helps us prove congruence without checking all three sides and all three angles.
How the HL Theorem Works
Using the HL Theorem involves a few simple steps. Let's break it down:
HL Theorem Formula
AC = XZ (hypotenuse)
BC = YZ (leg)
Then ΔABC ≅ ΔXYZ
When these conditions are met, the triangles are congruent.
Remember
The HL Theorem is different from other congruence theorems like SAS, ASA, or SSS because it specifically applies to right triangles.
HL Theorem Examples
Let's look at some examples of how the HL Theorem works:
Example 1: Basic Application
Triangle ABC and Triangle DEF are both right triangles. The hypotenuse of Triangle ABC is 5 cm, and one leg is 3 cm. The hypotenuse of Triangle DEF is 5 cm, and one leg is 3 cm. According to the HL Theorem, Triangle ABC ≅ Triangle DEF.
Example 2: With Measurements
Consider two right triangles where:
- Triangle 1: Hypotenuse = 10 units, Leg = 6 units
- Triangle 2: Hypotenuse = 10 units, Leg = 6 units
These triangles are congruent by the HL Theorem.
Example 3: Non-Example
Now consider:
- Triangle 1: Hypotenuse = 10 units, Leg = 6 units
- Triangle 2: Hypotenuse = 10 units, Leg = 8 units
These triangles are NOT congruent by the HL Theorem because although the hypotenuses are equal, the legs are different.
Practice Tip
When using the HL Theorem, always make sure both triangles are right triangles first. This is the most important requirement!
Practice Quiz
Test your understanding of the Hypotenuse Leg Theorem with this 5-question quiz.
Frequently Asked Questions
Here are answers to common questions about the Hypotenuse Leg Theorem:
Geometry Trivia
Discover interesting facts about geometry and triangles:
Ancient Geometry
The study of triangles dates back to ancient civilizations. The Egyptians used right triangles in constructing the pyramids, while Babylonians used them for astronomical calculations.
Triangles in Nature
Triangles are the strongest geometric shape, which is why they're used in construction like bridges and towers. You can also find triangles in honeycombs, crystal structures, and even in the way plants grow.
Pythagorean Theorem
The Pythagorean Theorem, which is fundamental to the HL Theorem, is one of the most famous mathematical theorems. There are over 400 different proofs of this theorem!
Real-World Applications
Triangle congruence theorems like the HL Theorem are used in architecture, engineering, computer graphics, and even in GPS technology to calculate distances and positions accurately.





