Identity Function - Definition, Examples, Quiz, FAQ, Trivia
Learn about the special math function that always returns the same value you put into it
What is the Identity Function?
The identity function is a special math function that always returns the same value that you put into it. It's like a mirror that reflects exactly what you show it, or a machine that gives you back exactly what you put in.
In mathematics, we write the identity function as: f(x) = x
This means that whatever number you put in for 'x', you get the same number out. If you put in 5, you get 5. If you put in 10, you get 10. It's that simple!
The identity function is important because it's like the "do nothing" operation in math. It doesn't change the value, just keeps it the same.
Identity Function Formula
For any input value x, the output is exactly the same.
Key Concept
The identity function is the simplest function possible. It's like looking in a mirror - you always see exactly what you put in!
How the Identity Function Works
Let's explore how the identity function works with different types of numbers:
With positive numbers:
f(5) = 5
f(12) = 12
f(100) = 100
With negative numbers:
f(-3) = -3
f(-10) = -10
With fractions:
f(½) = ½
f(¾) = ¾
With zero:
f(0) = 0
No matter what number you choose, the identity function gives you back exactly that same number. It's the mathematical equivalent of saying "same as before" or "no change."
Identity Function Table
| Input (x) | Function | Output f(x) |
|---|---|---|
| 2 | f(2) = 2 | 2 |
| 5 | f(5) = 5 | 5 |
| 10 | f(10) = 10 | 10 |
| -4 | f(-4) = -4 | -4 |
| 0 | f(0) = 0 | 0 |
| ½ | f(½) = ½ | ½ |
| 3.7 | f(3.7) = 3.7 | 3.7 |
Remember
The identity function works the same way for every number - it always returns exactly what you put in!
Examples of Identity Function
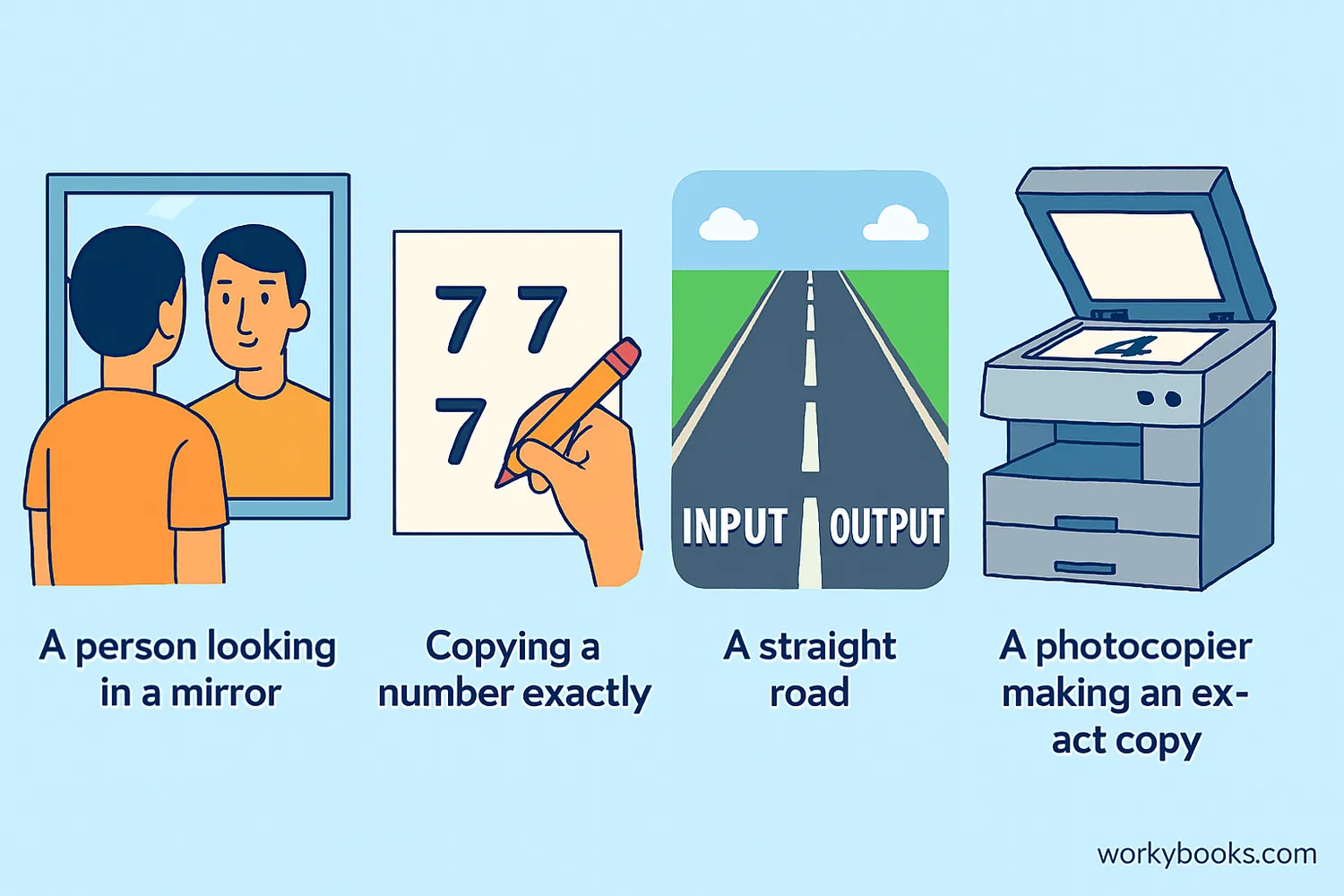
Let's look at some examples of how the identity function works in mathematics and in real life:
Example 1: Basic Number Identity
If f(x) = x, what is f(8)?
Solution: f(8) = 8
Example 2: Negative Numbers
If f(x) = x, what is f(-5)?
Solution: f(-5) = -5
Example 3: Fractions
If f(x) = x, what is f(¾)?
Solution: f(¾) = ¾
Real-Life Example 1: Mirror
A mirror shows you exactly what you look like - it's like the identity function for your appearance!
Real-Life Example 2: Photocopier
A photocopier set to 100% makes an exact copy of whatever you put in - just like the identity function.
Real-Life Example 3: Echo
In a perfect echo, you hear exactly what you said - just like the identity function gives back exactly what you put in.
Math Tip
The identity function is important in algebra because it helps us understand how other functions work by comparison.
Identity Function Practice Quiz
Test your understanding of the identity function with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about the identity function:
Math Trivia
Discover interesting facts about functions and mathematics:
Mathematical Origins
The concept of functions dates back to the 14th century, but it was the mathematician Leonhard Euler in the 18th century who first introduced the notation f(x) that we use today.
Identity in Computers
In computer programming, identity functions are used as "placeholder" functions when no transformation is needed. They help keep code clean and understandable.
Special Property
The identity function is the only function that is both one-to-one and onto at the same time for all real numbers. This makes it very special in advanced mathematics.
Universal Concept
The idea of an identity element exists in many areas of mathematics beyond just functions. There are identity elements for addition (0), multiplication (1), and even matrix operations.





