Partial Quotient - Definition, Examples, Quiz, FAQ, Trivia
Understanding Division with the Partial Quotient Method
What is Partial Quotient Division?
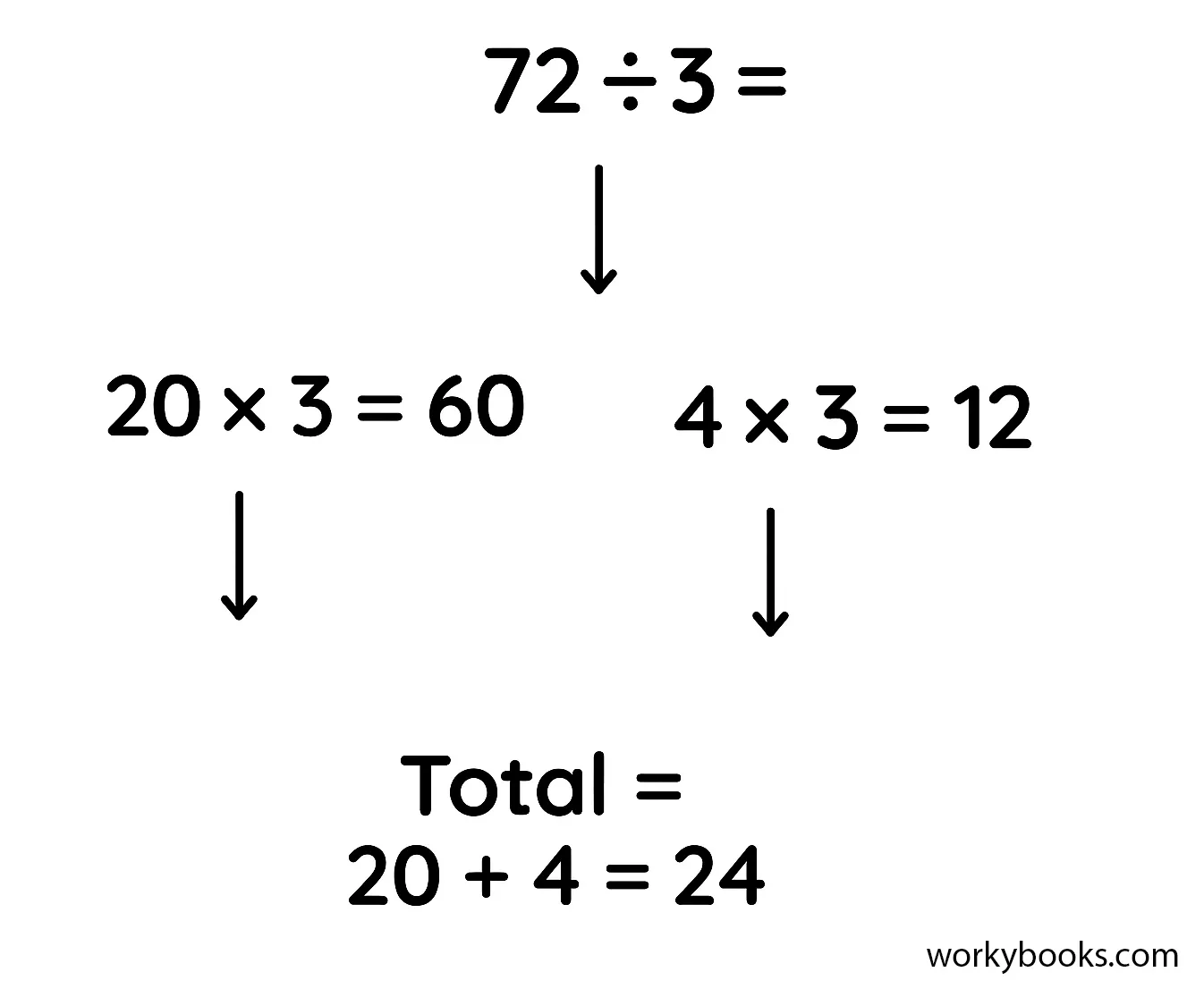
Partial quotient division is a helpful strategy for dividing large numbers. Instead of trying to solve a division problem all at once, we break it down into smaller, easier parts!
Think of it like sharing cookies with friends. If you have 84 cookies and want to share them equally among 7 friends, you could give each friend 10 cookies first (using 70 cookies), then share the remaining 14 cookies (2 more for each friend). That's the partial quotient method in action!
Math Tip!
The word "partial" means "part of a whole," and "quotient" is the answer to a division problem. So partial quotient means finding the answer in parts!
How Partial Quotient Division Works
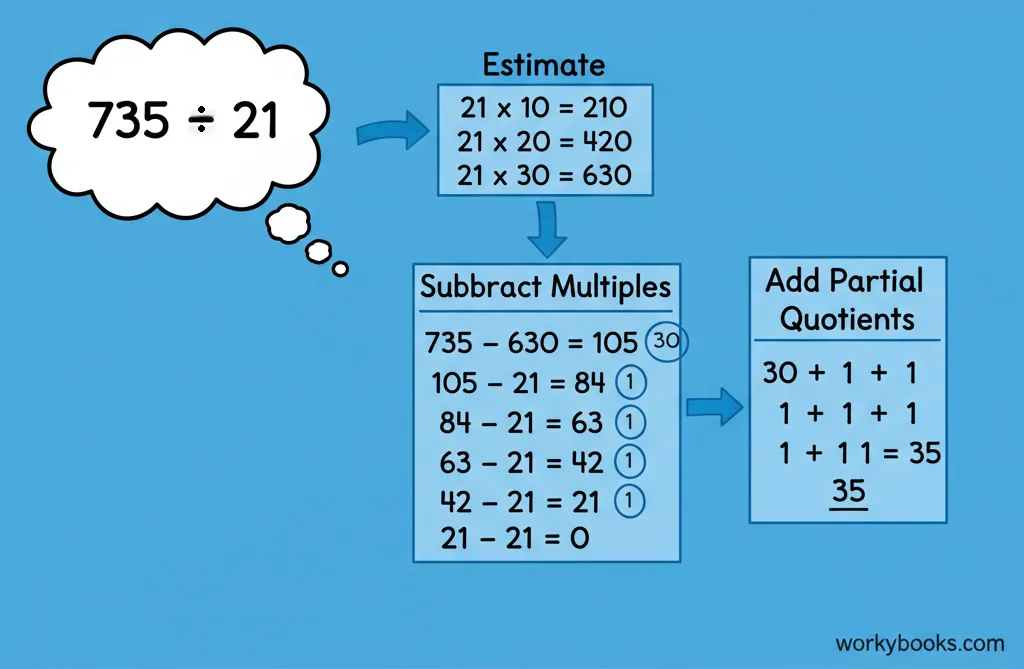
The partial quotient method works by using friendly numbers that are easy to multiply. Instead of figuring out the exact answer right away, we make smart estimates and subtract them from our total until we reach zero.
Estimate
Find an easy multiple of the divisor
Subtract
Subtract that multiple from the dividend
Record
Write down how many times you subtracted
Repeat
Continue with the remaining number
Add
Add up all your partial quotients
This method is great because you can use numbers that feel comfortable to you. Some people might subtract 10s, while others might subtract 5s or 2s. There's often more than one right way to solve the problem!
Step-by-Step Partial Quotient Method
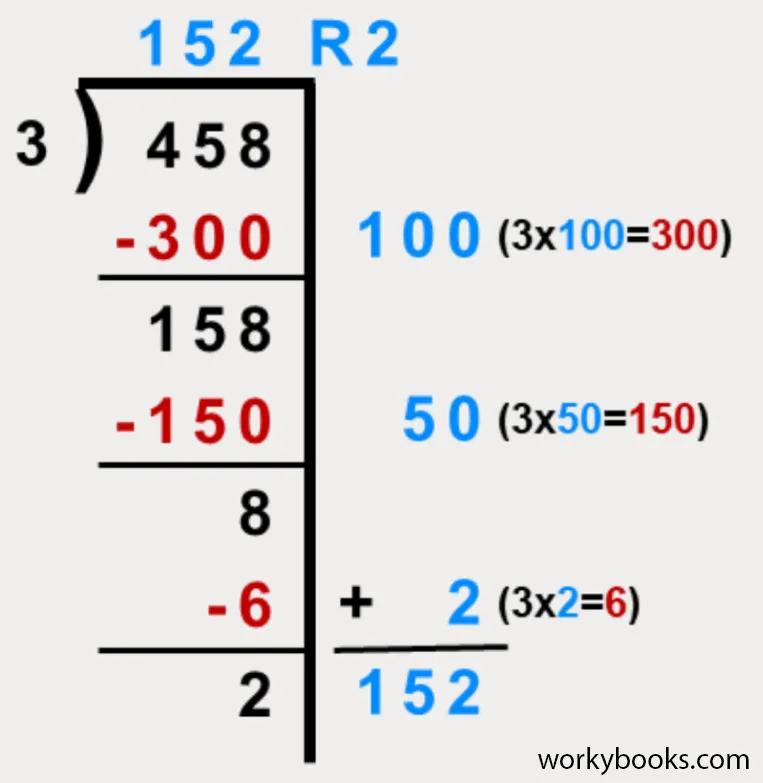
Let's solve 84 ÷ 7 using the partial quotient method step by step:
Notice how we broke the problem into two easier parts: first subtracting 70 (which is 7 × 10), then subtracting 14 (which is 7 × 2). When we added 10 + 2, we got our final answer of 12.
Remember!
You can use any multiples that make sense to you. The goal is to make the problem easier by breaking it into parts you can solve confidently.
Examples of Partial Quotient Division

Let's look at more examples to see how flexible the partial quotient method can be:
As you can see, there are often multiple ways to solve the same problem using partial quotients. The important thing is that your steps make sense and you eventually reach the correct answer.
Partial Quotient Division Quiz
Test your knowledge with this quiz! Answer all 5 questions to see how much you've learned about partial quotient division.
Frequently Asked Questions
Here are answers to some common questions about partial quotient division:
Math Facts About Division
Discover some fascinating facts about division and mathematics!
Historical Division
The concept of division dates back to ancient civilizations like the Egyptians and Babylonians, who used various methods to solve division problems over 4,000 years ago!
Division by Zero
Division by zero is impossible in mathematics. If you try to divide any number by zero, the result is undefined. This is one of the fundamental rules of math!
Division Words
The word "division" comes from the Latin word "dividere," which means "to separate." The diagonal line in the division symbol (÷) is thought to represent a fraction with dots above and below.
Real-World Division
We use division every day without realizing it! When you share snacks with friends, split bills, or measure ingredients for a recipe, you're using division concepts.





