Perpendicular Bisector Theorem - Definition, Examples, Quiz, FAQ, Trivia
Discover how perpendicular bisectors help us understand equal distances in geometry!
What is a Perpendicular Bisector?
A perpendicular bisector is a special line that divides another line segment into two equal parts at a perfect right angle (90 degrees). Think of it like cutting a sandwich exactly in half with a perfectly straight cut!
The word "perpendicular" means at a right angle, and "bisector" means something that cuts into two equal parts. So a perpendicular bisector cuts a line segment into two equal halves at a 90-degree angle.
Math Fact!
Perpendicular bisectors are used in many real-world applications, from architecture and construction to navigation and even sports field markings!
The Perpendicular Bisector Theorem
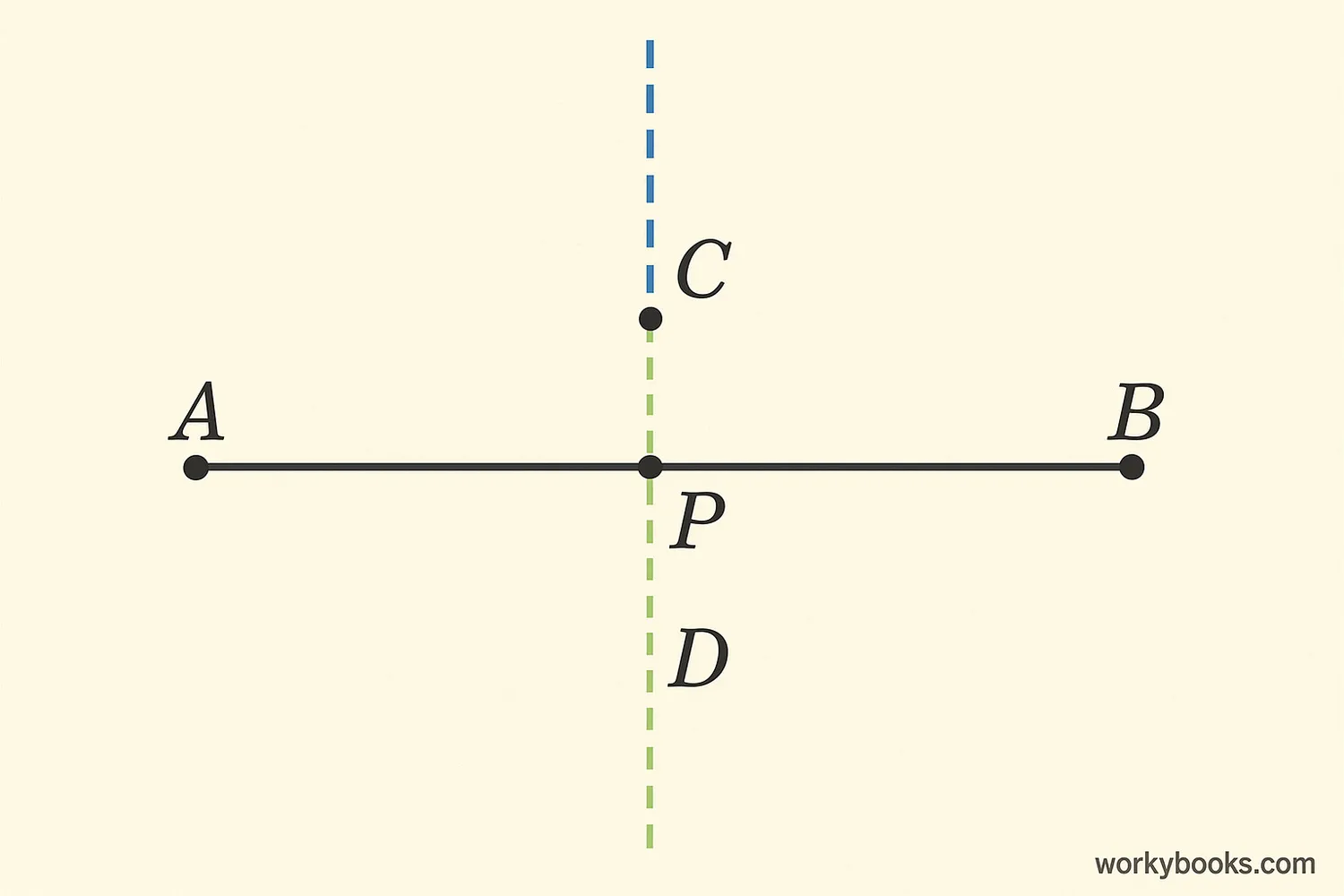
The Perpendicular Bisector Theorem is an important rule in geometry that tells us:
If a point lies on the perpendicular bisector of a segment, then it is equidistant (the same distance) from the segment's two endpoints.
This means that if you have a line segment AB, and point C is on its perpendicular bisector, then the distance from C to A will equal the distance from C to B.
Equal Distances
Any point on the perpendicular bisector is exactly the same distance from both endpoints of the segment.
Two-Way Rule
The theorem works both ways: if a point is equidistant from two endpoints, it lies on the perpendicular bisector.
Construction
This theorem helps us construct perpendicular bisectors using just a compass and straightedge.
Understanding the Theorem Proof
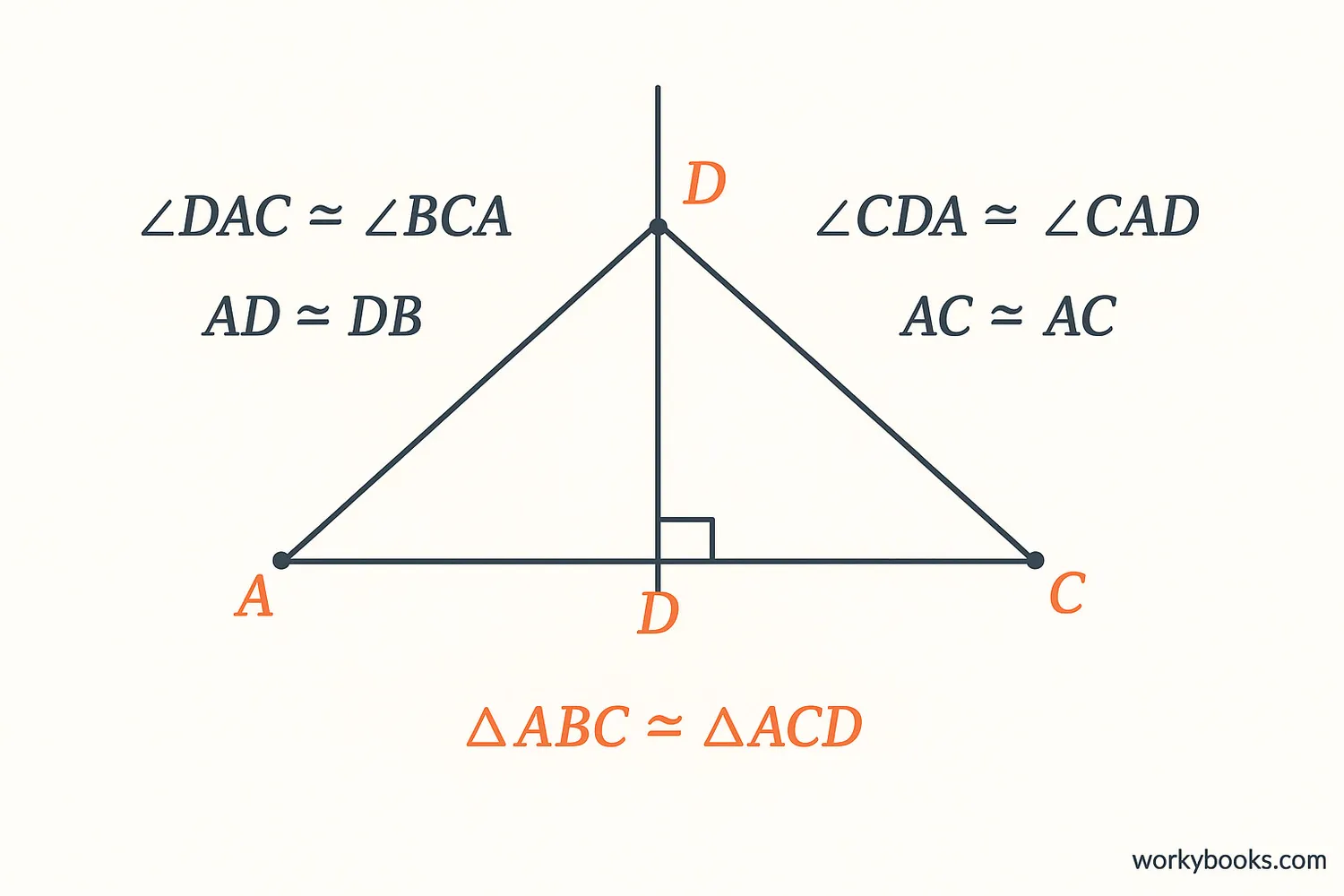
We can prove the Perpendicular Bisector Theorem using congruent triangles. Here's how it works:
Given
Line CD is the perpendicular bisector of segment AB, meeting at point M (the midpoint)
Construct
Pick any point P on the perpendicular bisector CD and draw segments to A and B
Compare
Triangles PMA and PMB are congruent by SAS (Side-Angle-Side) congruence
Conclude
Since the triangles are congruent, PA must equal PB
This proof shows us why the theorem works: because we create two identical triangles, which means the distances from any point on the bisector to the endpoints must be equal.
Examples of the Theorem
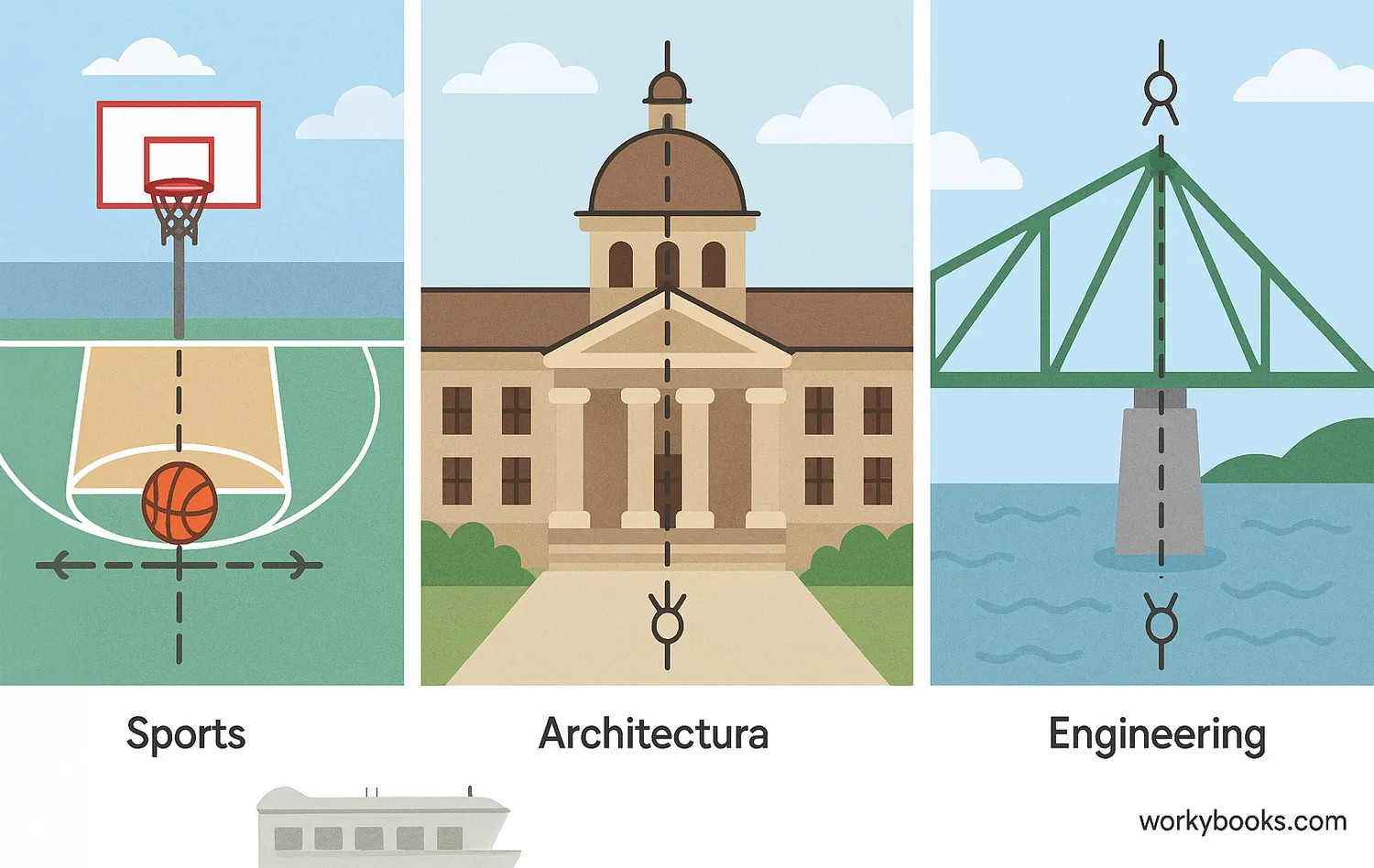
Let's look at some examples of how the Perpendicular Bisector Theorem works:
Sports Fields
The center line in soccer or football is a perpendicular bisector of the halfway line between goals. All points on this line are equidistant from both goals.
Architecture
When building a bridge, engineers use perpendicular bisectors to ensure support structures are evenly placed between anchor points.
Navigation
If you need to find a point that's exactly between two locations (and equally distant from both), you're looking for a point on the perpendicular bisector.
Example Problem
Segment AB is 10 cm long. Point P lies on the perpendicular bisector of AB. If the distance from P to A is 7 cm, what is the distance from P to B?
Answer: According to the theorem, the distance from P to B must also be 7 cm!
Geometry Quiz
Test your knowledge about perpendicular bisectors with this quiz! Answer all 5 questions to see how much you've learned.
Frequently Asked Questions
Here are answers to some common questions about the Perpendicular Bisector Theorem:
Math Trivia
Discover some interesting facts about perpendicular bisectors and geometry!
Ancient Origins
The concept of perpendicular bisectors dates back to ancient Greek mathematicians like Euclid, who described them in his famous work "Elements" around 300 BCE.
Space Applications
NASA engineers use principles similar to the perpendicular bisector theorem when calculating trajectories and orbital paths for spacecraft.
Nature's Geometry
Honeybees use geometric principles similar to perpendicular bisectors when building their honeycombs, creating perfectly hexagonal cells with precise angles.
Tech Connections
Your smartphone uses geometric algorithms based on principles like the perpendicular bisector theorem for features like GPS navigation and augmented reality.





