Translation - Definition, Examples, Quiz, FAQ, Trivia
Learn how to slide shapes and functions with geometric translations
What is Translation in Math?

Translation is a type of geometric transformation that slides a shape or function from one position to another without rotating, flipping, or changing its size. It's like moving a book across a table - the book stays the same shape and size, just its position changes.
In math, we use translations to:
- Move points on a coordinate grid
- Slide entire shapes without changing them
- Shift graphs of functions left, right, up, or down
Translations are rigid transformations because they preserve the size and shape of the original figure. Every point in the shape moves the same distance in the same direction.
Key Concept
Translation moves every point of a shape the same distance in the same direction without changing the shape's size or orientation.
Understanding Translation Vectors
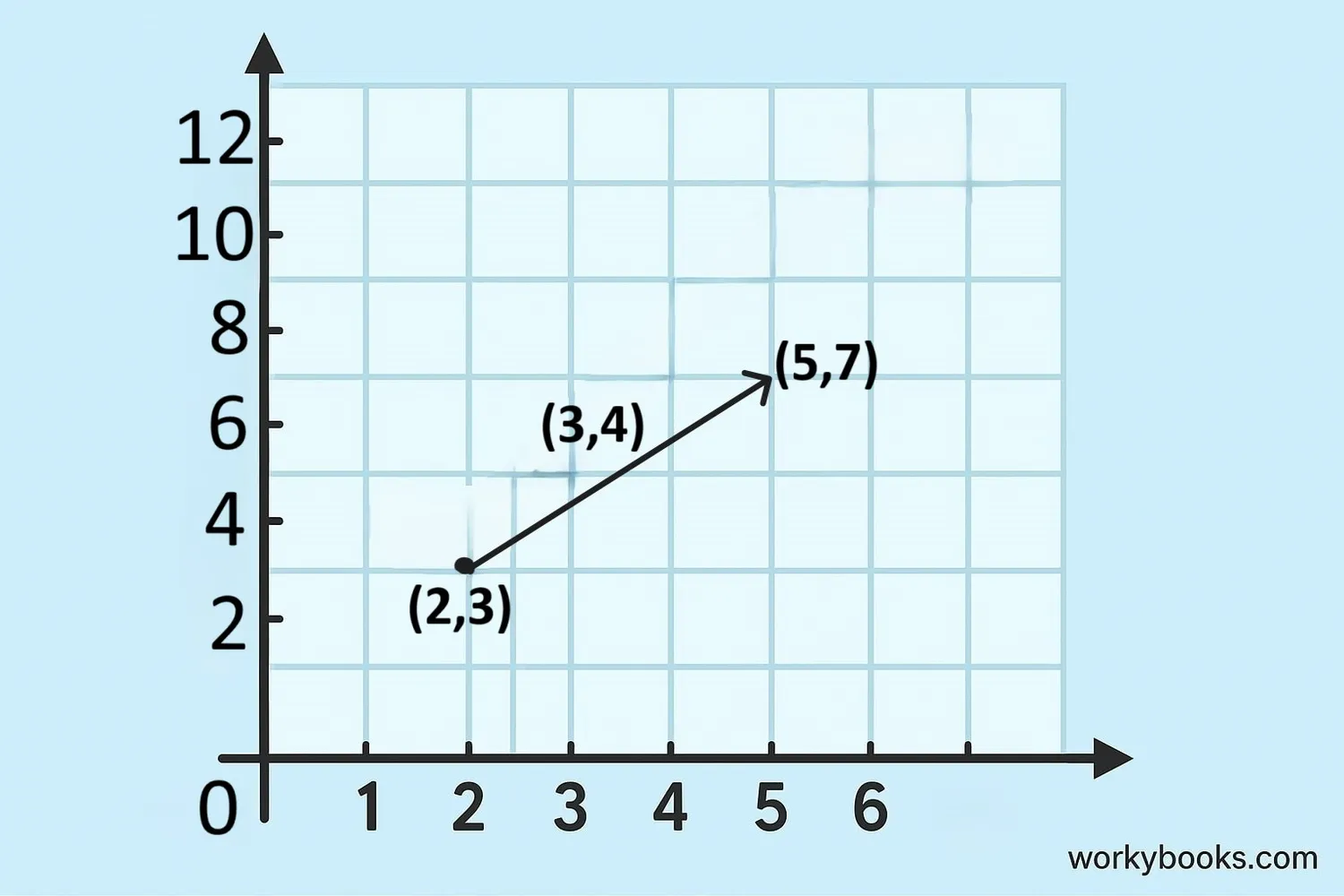
A translation vector tells us exactly how far and in what direction to move each point of a shape. It has two components:
Translation Vector
Where 'a' is the horizontal movement and 'b' is the vertical movement
- Positive 'a' → Move right
- Negative 'a' → Move left
- Positive 'b' → Move up
- Negative 'b' → Move down
Example: To translate a point (x, y) with vector (3, -2):
New position = (x + 3, y - 2)
Remember
Vectors describe both the distance and direction of movement. The length of the vector arrow shows how far the shape moves.
Translating Geometric Shapes
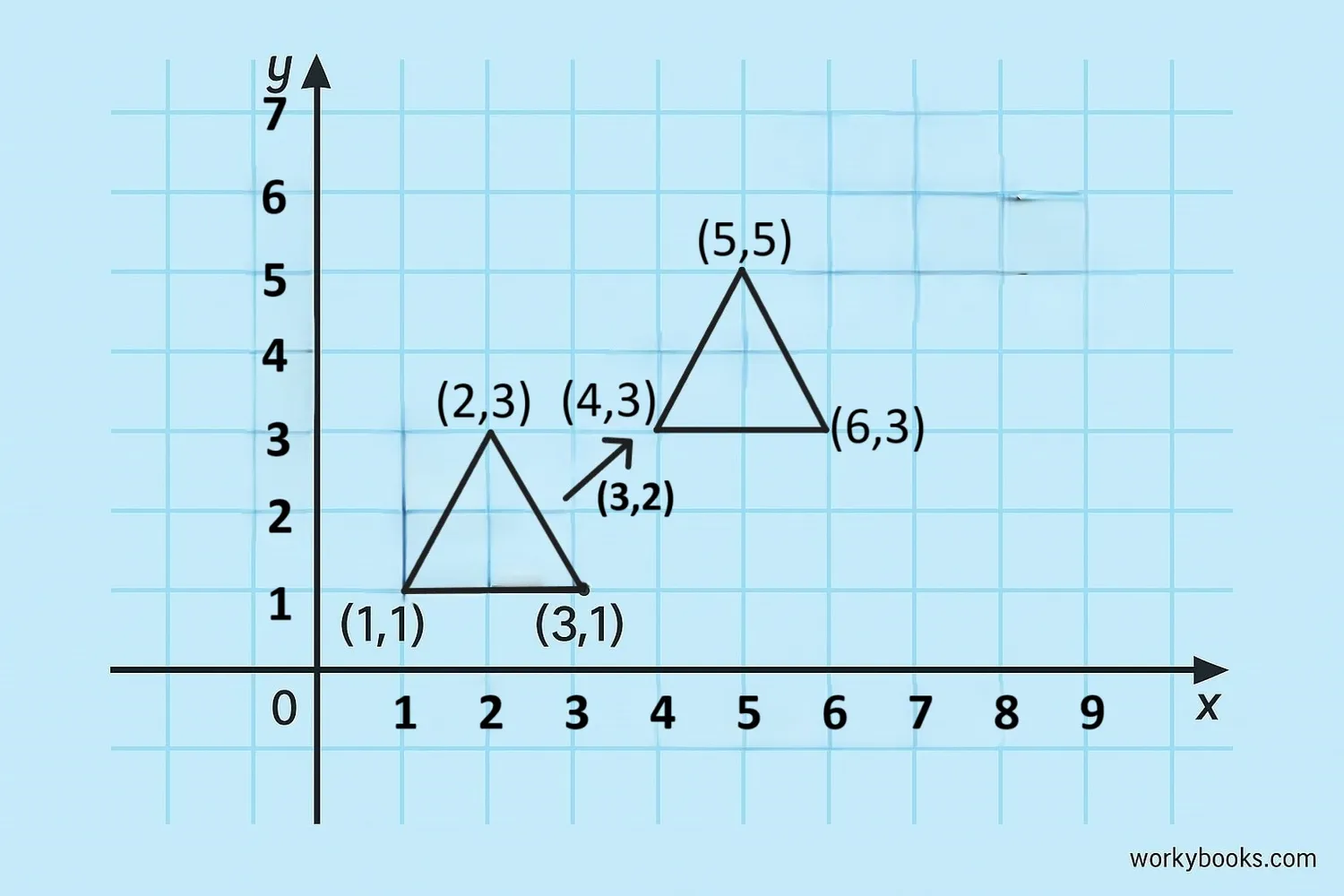
Translating shapes involves moving every point of the shape according to the translation vector. Here's how to translate a triangle:
Step-by-Step Example:
- Identify the vertices: Triangle ABC at A(1,1), B(3,1), C(2,3)
- Determine the translation vector: (3,2)
- Add vector components to each vertex:
- A(1+3, 1+2) = A'(4,3)
- B(3+3, 1+2) = B'(6,3)
- C(2+3, 3+2) = C'(5,5)
- Plot the new points and connect them to form triangle A'B'C'
The original and translated shapes are congruent - same size and shape, just in a different location.
Horizontal Translation
Moving a shape left or right without changing its vertical position.
Vector: (a, 0)
Vertical Translation
Moving a shape up or down without changing its horizontal position.
Vector: (0, b)
Diagonal Translation
Moving a shape both horizontally and vertically at the same time.
Vector: (a, b)
Translating Functions
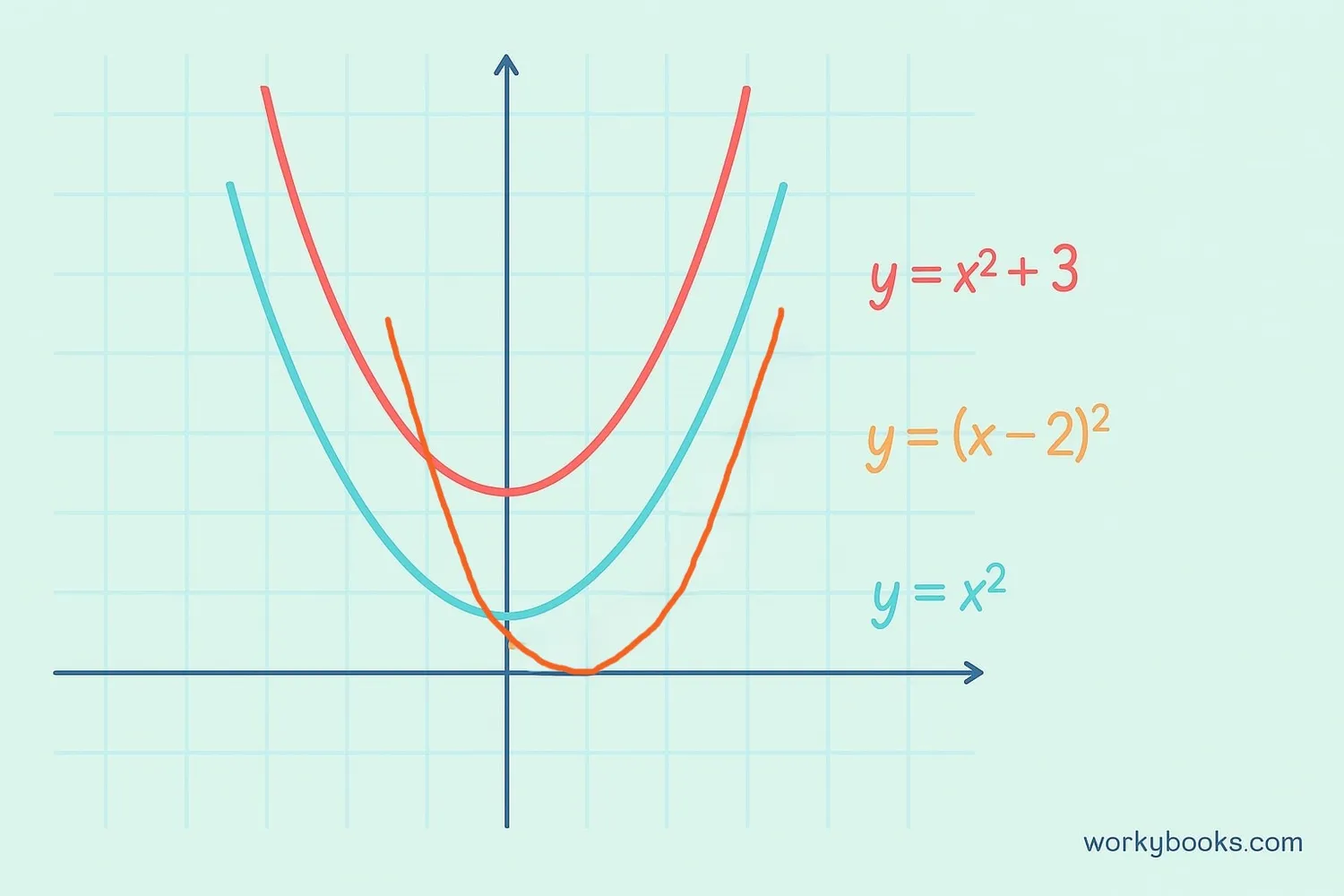
We can also translate the graphs of functions. This shifts the entire graph without changing its shape.
Function Translation Rules
Where 'h' is the horizontal shift and 'k' is the vertical shift
- f(x - h) shifts the graph right by h units
- f(x + h) shifts the graph left by h units
Vertical Translation:
- f(x) + k shifts the graph up by k units
- f(x) - k shifts the graph down by k units
Example:
Original function: f(x) = x²
Translated: g(x) = (x - 3)² + 2
This is shifted 3 units right and 2 units up
Remember
Horizontal translation is counter-intuitive: f(x - h) moves the graph to the right, not left!
Translation Practice Quiz
Test your understanding of translations with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about geometric translations:
Math Transformation Trivia
Discover interesting facts about geometric transformations:
Ancient Origins
The concept of geometric transformations dates back to ancient Greece. Euclid's "Elements" (300 BC) described transformations, though the formal study developed much later.
Crystal Structures
Translations are fundamental in crystallography. The repeating patterns in crystals are described by translation symmetry, where the structure looks identical after certain shifts.
Art and Design
M.C. Escher's famous artwork uses translations and other transformations to create mesmerizing patterns that repeat and transform across the canvas.
Video Game Graphics
Translation is one of the most common operations in computer graphics. Game engines perform millions of translations per second to move characters and objects.


