Isolate Variables - Definition, Examples, Quiz, FAQ, Trivia
Learn to solve equations by isolating variables with step-by-step explanations and practice activities
What Does "Isolate" Mean?

In algebra, to isolate a variable means to get it alone on one side of an equation. Think of it like solving a mystery - we want to find the value of our variable (like x or y) by itself.
Why do we isolate variables? It helps us solve equations and find unknown values. When we isolate a variable, we discover its value by performing operations that "undo" what's being done to it.
Key idea: An equation is like a balanced scale. Whatever we do to one side, we must do to the other to keep it balanced. When we isolate the variable, we're finding out what makes both sides equal.
Key Concept
Isolating a variable means getting it by itself on one side of the equation, usually the left side, using inverse operations.
How to Isolate a Variable
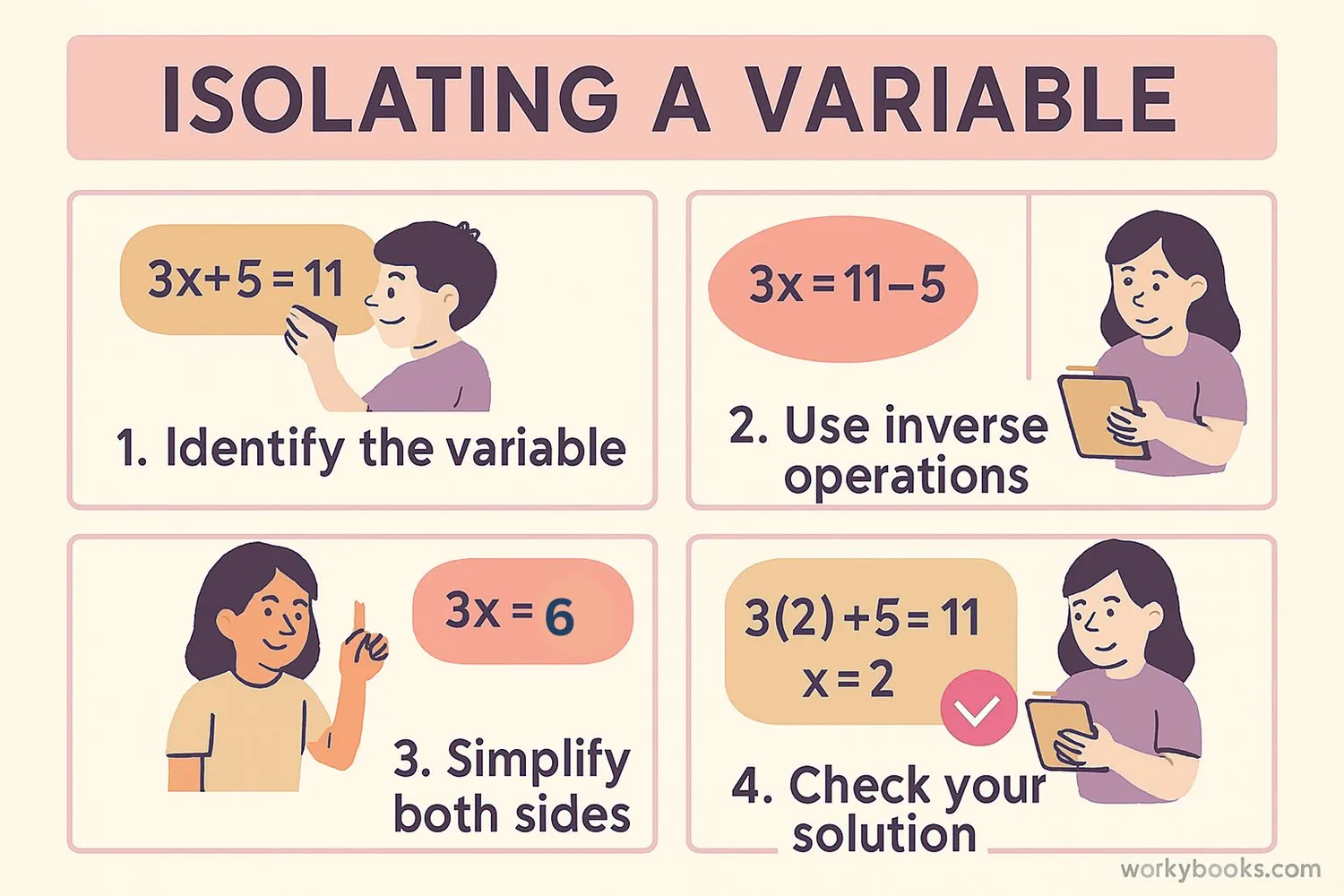
Isolating a variable is like solving a puzzle. We use inverse operations to "undo" what's being done to the variable. Inverse operations are opposite operations - addition and subtraction are inverses, multiplication and division are inverses.
Inverse Operations
× ⟷ ÷
Use the opposite operation to isolate your variable
Step-by-Step Guide:
Remember
Whatever you do to one side of the equation, you must do to the other side to keep it balanced.
Examples of Isolating Variables
Let's look at some examples of isolating variables. Remember to perform the same operation on both sides of the equation!
Example 1: Addition Equation
To isolate x, subtract 8 from both sides:
Example 2: Subtraction Equation
To isolate y, add 4 to both sides:
Example 3: Multiplication Equation
To isolate z, divide both sides by 3:
Example 4: Two-Step Equation
Step 1: Subtract 5 from both sides:
Step 2: Divide both sides by 2:
Practice Tip
Always check your solution by substituting it back into the original equation to verify it works.
Isolating Variables Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about isolating variables:
Math Trivia
Discover interesting facts about algebra and equations:
Ancient Algebra
The word "algebra" comes from the Arabic word "al-jabr" meaning "reunion of broken parts." It was first used in the 9th century by Persian mathematician Muhammad ibn Musa al-Khwarizmi.
Variables in Space
NASA uses algebra to calculate rocket trajectories, orbital paths, and mission durations. Without algebra, space travel would be impossible!
Longest Equation
The longest mathematical equation ever written was a physics problem that required about 200 terabytes of storage! It was created to understand quantum mechanics.
X Marks the Spot
The use of "x" as a variable was popularized by mathematician René Descartes in the 17th century. Before that, mathematicians used words or other symbols to represent unknowns.





