Undefined Slope - Definition, Examples, Quiz, FAQ, Trivia
Learn why vertical lines have undefined slope and how to work with them in mathematics
What is Undefined Slope?
Slope tells us how steep a line is. We usually calculate it using the formula:
Slope Formula
Where m is the slope, (x₁, y₁) and (x₂, y₂) are two points on the line
For a vertical line, the x-coordinates of any two points are the same. This means (x₂ - x₁) = 0. Since division by zero is undefined in math, the slope becomes undefined.
So whenever you see a perfectly vertical line, you know it has undefined slope!
Key Concept
Vertical lines have undefined slope because their x-values don't change, making the denominator zero in the slope formula.
Understanding Vertical Lines
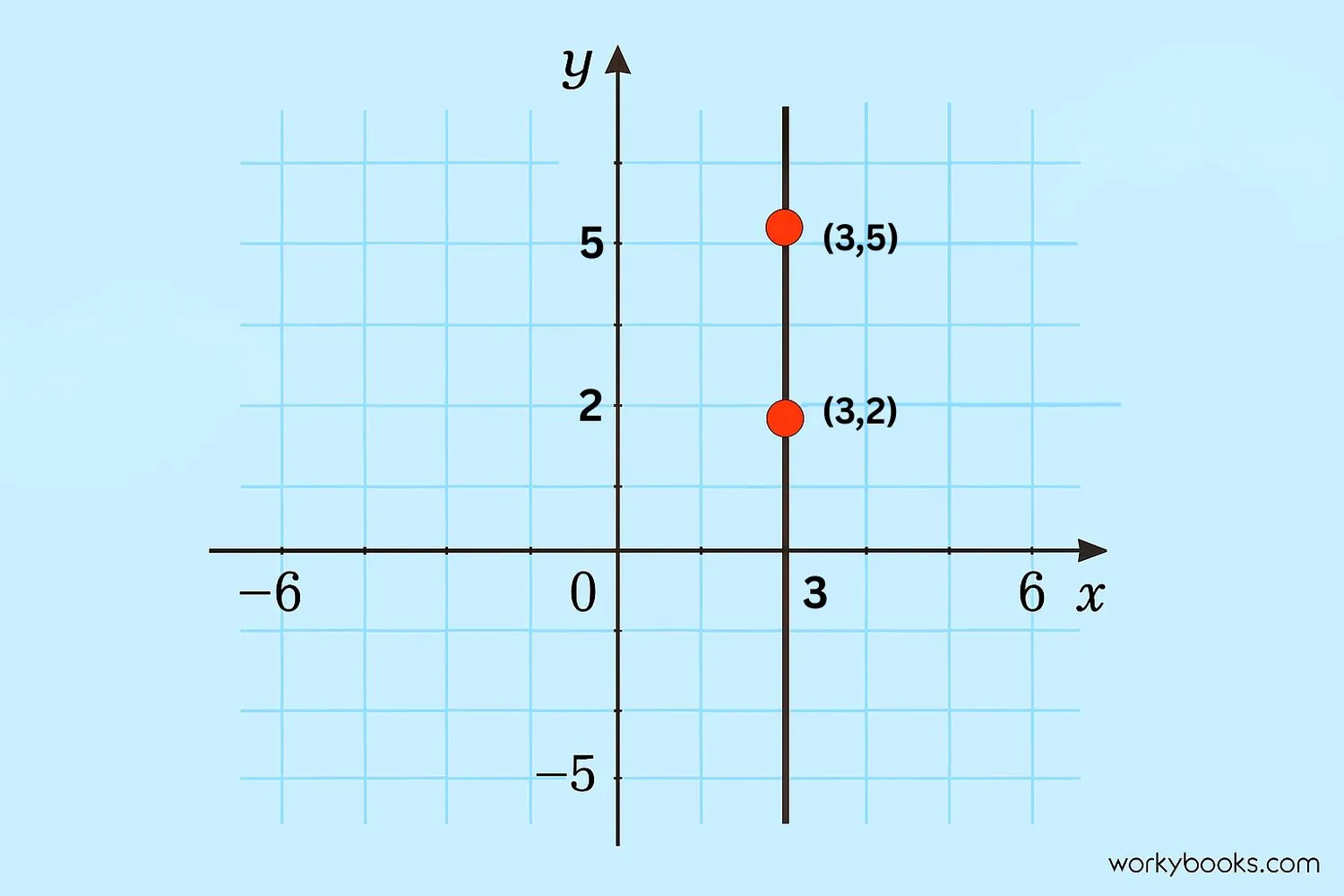
A vertical line goes straight up and down. Unlike other lines, it doesn't slant at all. Here's what makes vertical lines special:
• All points on a vertical line have the same x-coordinate
• The x-value never changes, no matter how far up or down you go
• The slope formula gives division by zero, so we say the slope is undefined
Think of it like climbing a ladder - you're going straight up without moving sideways at all. That's what makes the slope undefined!
Remember
Horizontal lines have zero slope, vertical lines have undefined slope. This is an important difference!
Vertical Line Equation
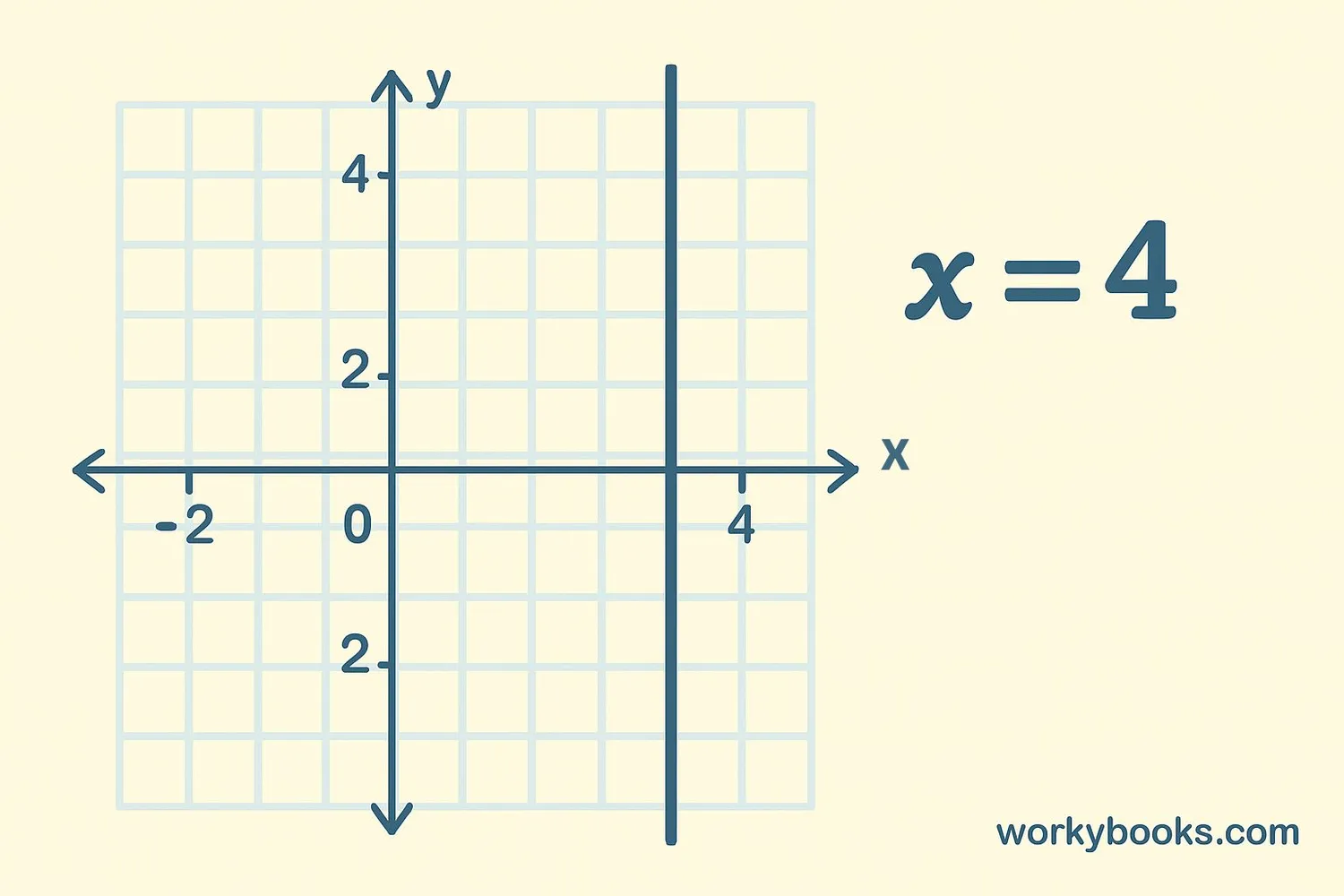
Since all points on a vertical line have the same x-coordinate, we write its equation as:
Equation of a Vertical Line
Where 'a' is the x-coordinate where the line crosses the x-axis
• The line x = 3 passes through all points where x is 3: (3,0), (3,1), (3,2), etc.
• The line x = -2 passes through (-2,0), (-2,1), (-2,2), etc.
Notice that the equation doesn't include y at all. That's because y can be any value - the line goes on forever in the up and down directions!
Writing Tip
When you see an equation like x=5, you immediately know it's a vertical line with undefined slope.
Real-World Examples
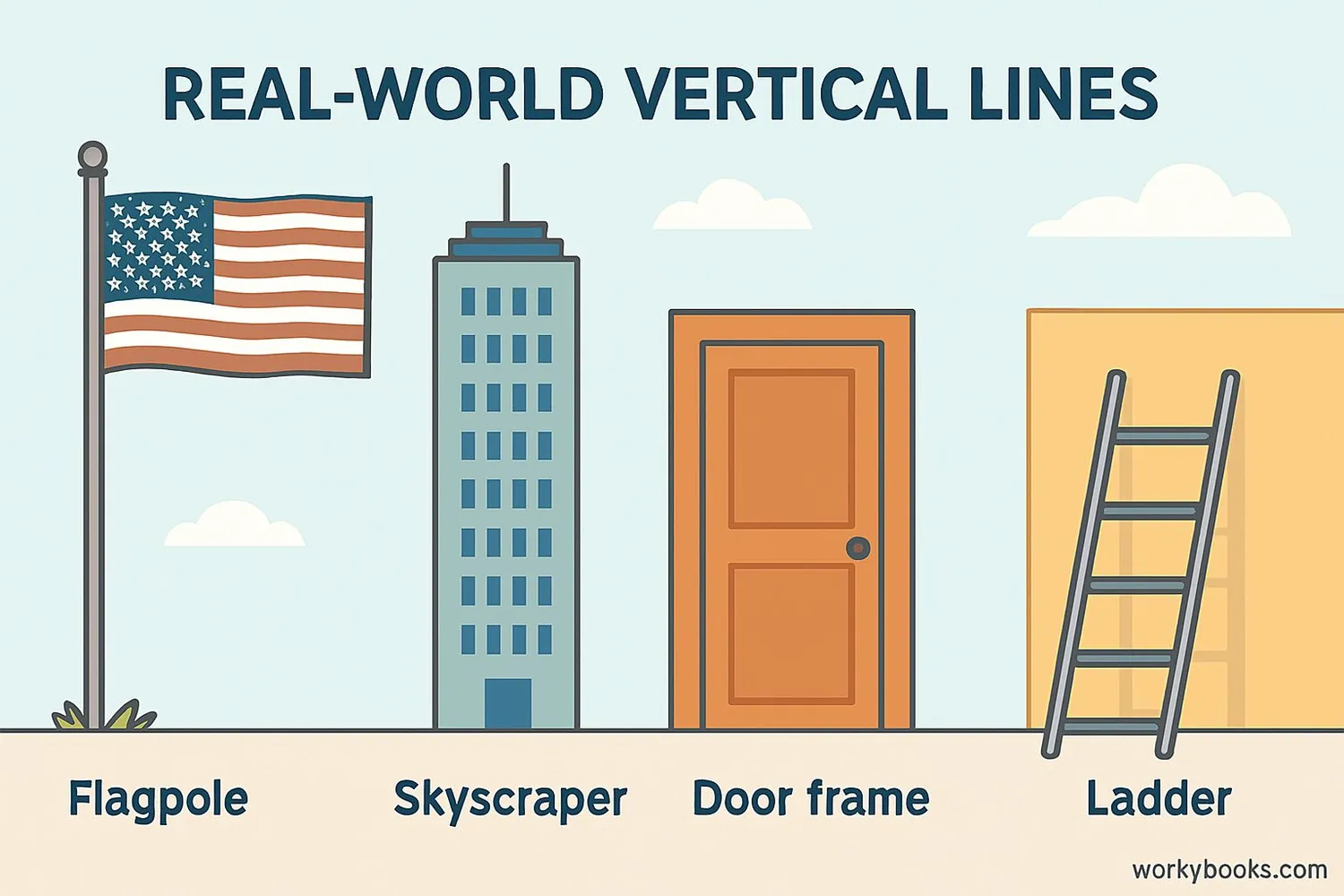
Let's look at some examples of undefined slope in real life:
Example 1: A flagpole
Solution: A flagpole stands perfectly straight up. Its slope is undefined because it doesn't lean in any direction.
Example 2: The edge of a door
Solution: The sides of a door frame are vertical lines. They have undefined slope.
Example 3: A ladder standing straight
Solution: If a ladder isn't leaning, it's vertical and has undefined slope.
Example 4: The line between points (2,3) and (2,7)
Solution: Since both points have x=2, this is a vertical line. The slope is undefined because (7-3)/(2-2) = 4/0, which is undefined.
Practice finding vertical lines around you - buildings, trees, or even the sides of your notebook!
Learning Tip
Vertical lines are the only lines with undefined slope. All other lines have a defined slope value.
Undefined Slope Quiz
Test your understanding of undefined slope with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about undefined slope:
Math Trivia
Discover interesting facts about slopes and mathematics:
Ancient Origins
The concept of slope dates back to ancient Egypt, where builders used slope calculations to construct pyramids with precise angles.
Steepest Streets
Baldwin Street in New Zealand is the world's steepest residential street with a slope of 35%! That means for every 100 meters horizontally, it rises 35 meters vertically.
Space Exploration
NASA engineers use slope calculations to plan rocket launches. The slope of the rocket's path determines how much fuel is needed to escape Earth's gravity.
Engineering Marvel
The Millau Viaduct in France is the world's tallest bridge. Engineers used precise slope calculations to create its gently sloping deck that's 270 meters above the river at its highest point.





