Angular Velocity - Definition, Examples, Quiz, FAQ, Trivia
Discover how spinning objects move and how we measure their rotation!
What is Angular Velocity?
Angular velocity describes how fast something is spinning or rotating. It tells us how quickly an object turns around a fixed point or axis. Imagine a merry-go-round at the playground - angular velocity measures how fast it's spinning.
When something rotates, different points move at different speeds. The center might not move much, but the outer edges move faster. Angular velocity helps us understand this spinning motion in a simple way.
Key Point
Angular velocity measures rotational speed, not how fast something is moving in a straight line.
Angular Velocity Formula
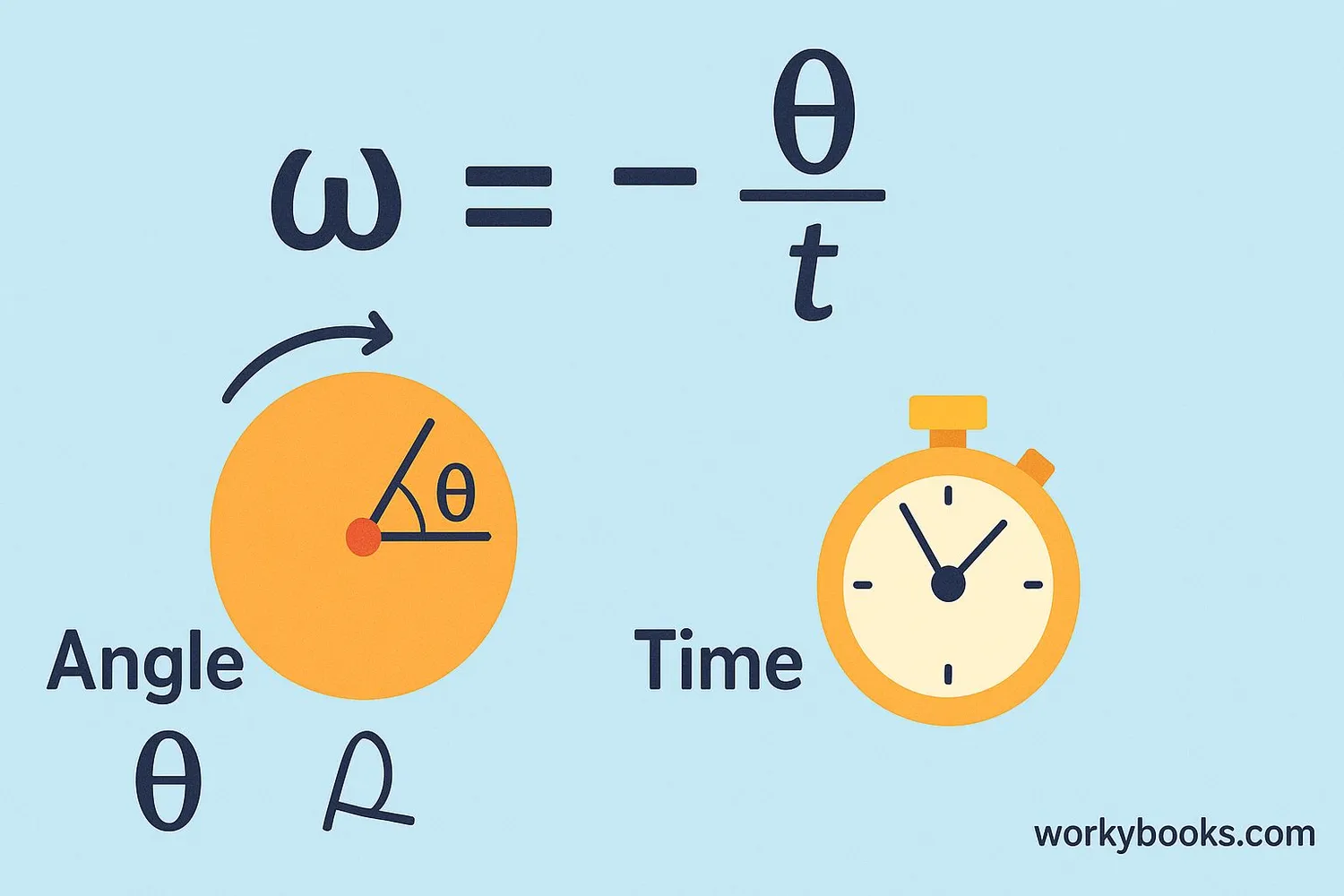
We calculate angular velocity using a simple formula:
Where:
• ω (omega) is the angular velocity
• θ (theta) is the angle rotated (in radians or degrees)
• t is the time taken to rotate through that angle
For example, if a wheel completes one full rotation (360° or 2π radians) in 2 seconds, its angular velocity would be:
360° / 2 seconds = 180° per second, or
2π radians / 2 seconds = π radians per second
Remember
Scientists usually measure angles in radians for angular velocity calculations. There are 2π radians in a full circle (360°).
Angular Velocity vs Linear Velocity
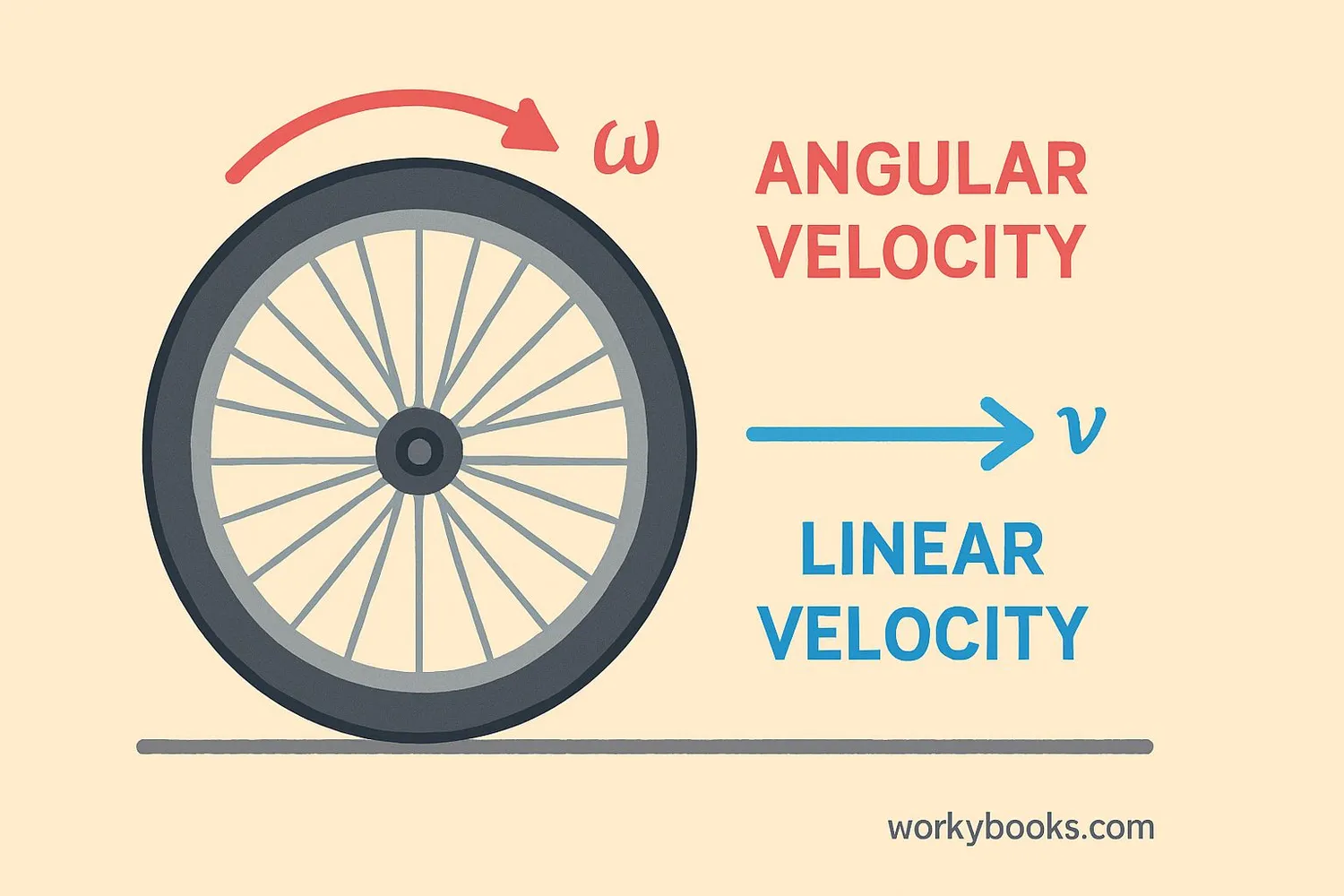
Angular velocity and linear velocity are related but different concepts:
| Angular Velocity | Linear Velocity |
|---|---|
| Measures rotational speed | Measures straight-line speed |
| Measured in degrees/sec or radians/sec | Measured in meters/sec or miles/hour |
| Describes how fast something spins | Describes how fast something moves from point A to B |
| Same for all points on a rotating rigid body | Different at different distances from the center |
They're connected by this relationship:
Linear Velocity = Angular Velocity × Radius
This means points farther from the center of rotation move faster in a straight line even though they have the same angular velocity as points closer to the center.
Angular Velocity Units

Angular velocity can be measured in several different units:
Radians per Second
The scientific standard unit (rad/s)
Degrees per Second
Common in everyday measurements (°/s)
Revolutions per Minute
Often used for engines and turntables (RPM)
Here's how to convert between these units:
• 1 revolution = 360° = 2π radians
• 1 RPM = 6° per second = π/30 radians per second
Scientists prefer radians because they simplify many physics calculations, especially when connecting angular motion to linear motion.
Angular Velocity Examples
Angular velocity is all around us! Here are some common examples:
Earth's Rotation
Earth rotates 360° in 24 hours, giving us an angular velocity of 15° per hour
Record Players
Vinyl records typically play at 33⅓, 45, or 78 RPM
Car Engines
Car engines might spin at 2000-3000 RPM when cruising
Other examples include:
• Bicycle wheels spinning as you ride
• Ceiling fans circulating air
• Wind turbines generating electricity
• Figure skaters spinning during a performance
• Merry-go-rounds at the playground
Understanding angular velocity helps engineers design better machines and helps scientists understand how planets and galaxies move!
Angular Velocity Quiz
Test your knowledge with this angular velocity quiz! Answer all 5 questions to see how much you've learned.
Frequently Asked Questions
Here are answers to some common questions about angular velocity:
Angular Velocity Trivia
Discover some amazing facts about angular velocity!
Neutron Stars
Some neutron stars (called pulsars) rotate hundreds of times per second! That's an angular velocity of over 2000 radians per second.
Animal Spinners
Some flies can beat their wings over 1000 times per second, achieving incredible angular velocities that allow them to hover and change direction quickly.
Ultracentrifuges
Scientific ultracentrifuges can spin at over 150,000 RPM, creating forces millions of times stronger than gravity to separate tiny particles.
Baseball Physics
A major league curveball spins at about 1800-2000 RPM. This spin creates air pressure differences that make the ball curve unexpectedly.





