Hexadecimal to Binary (Hex to Bin) - Definition, Examples, Quiz, FAQ, Trivia
Learn to convert between hexadecimal and binary number systems with easy explanations and practice activities
Understanding Number Systems
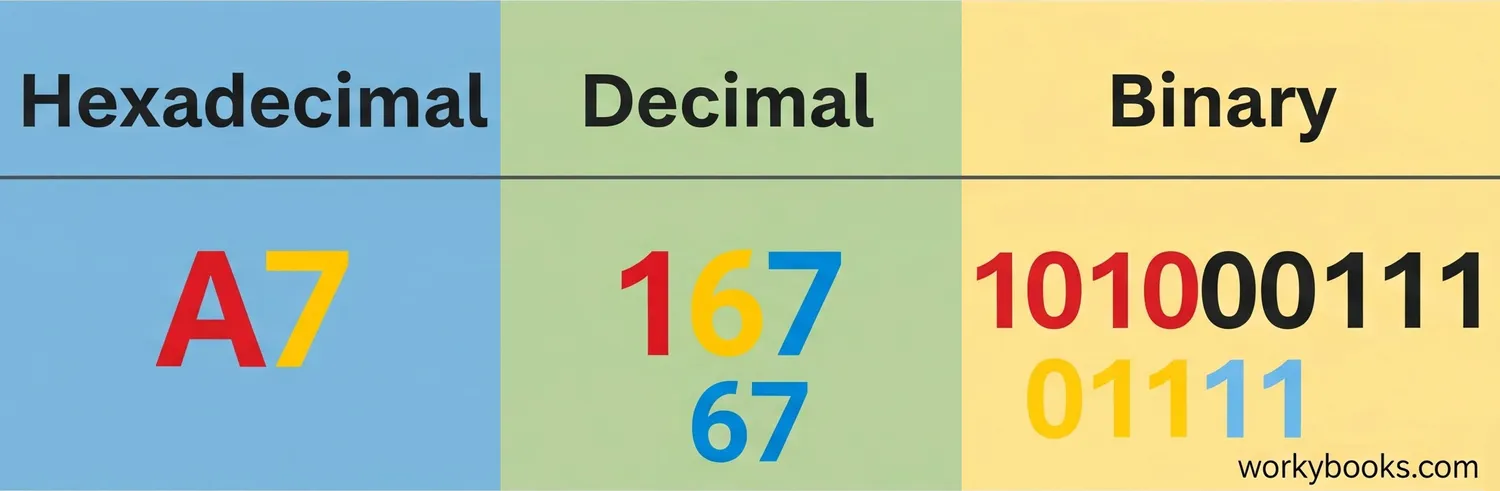
Number systems are different ways to represent and work with numbers. The three most important systems in computer science are:
Binary (Base-2): Uses only two digits - 0 and 1. This is the language computers understand.
Decimal (Base-10): Uses ten digits - 0 to 9. This is the system we use every day.
Hexadecimal (Base-16): Uses sixteen digits - 0 to 9 and A to F. This system is a shortcut for binary.
Why do we use hexadecimal? It's much easier to read and write than long binary numbers. Since each hexadecimal digit represents four binary digits (bits), we can convert between them easily.
Key Concept
Each hexadecimal digit corresponds to a group of four binary digits (bits). This makes conversion between hex and binary straightforward.
How to Convert Hexadecimal to Binary
Converting hexadecimal to binary is simple when you follow these steps:
Conversion Formula
Convert each hexadecimal digit to its 4-bit binary equivalent
Separate Digits
Break the hexadecimal number into individual digits
Convert Each Digit
Convert each hex digit to its 4-bit binary equivalent
Combine Results
Join all the binary groups together
Example: Convert A3 to binary
Step 1: Separate digits → A and 3
Step 2: Convert each digit:
A = 1010
3 = 0011
Step 3: Combine → 10100011
So hexadecimal A3 equals binary 10100011. Simple!
Remember
Each hexadecimal digit must be converted to exactly four binary digits. Add leading zeros if needed to make four bits.
Hexadecimal to Binary Conversion Charts
Conversion charts help us quickly find equivalent values without calculating each time. Here are two useful charts for converting hexadecimal to binary:
Hexadecimal to Binary Conversion Chart
| Hexadecimal | Binary |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| A | 1010 |
| B | 1011 |
| C | 1100 |
| D | 1101 |
| E | 1110 |
| F | 1111 |
Hexadecimal Numbers to Binary Conversion
| Hexadecimal | Binary |
|---|---|
| 10 | 0001 0000 |
| 20 | 0010 0000 |
| 2A | 0010 1010 |
| FF | 1111 1111 |
| 1F | 0001 1111 |
| AB | 1010 1011 |
| C0 | 1100 0000 |
Chart Tip
Notice how each hexadecimal digit corresponds to exactly four binary digits? This pattern makes conversion easy to remember!
Conversion Examples

Let's practice conversion with some real-world examples:
Example 1: Convert the hexadecimal number 4B to binary
Solution:
4 = 0100
B = 1011
Combined: 01001011 → 01001011
Example 2: Convert F0 to binary
Solution:
F = 1111
0 = 0000
Combined: 11110000 → 11110000
Example 3: Convert 1A3 to binary
Solution:
1 = 0001
A = 1010
3 = 0011
Combined: 000110100011 → 000110100011
Practice converting these hexadecimal values: 2C, 7E, D5, and FF
Conversion Tip
To convert binary back to hexadecimal, group the binary digits into sets of four (starting from the right) and convert each group to its hex equivalent.
Conversion Practice Quiz
Test your conversion skills with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about hexadecimal and binary conversion:
Number System Trivia
Discover interesting facts about number systems:
Origin of Hexadecimal
The hexadecimal system was first introduced in the 1950s by computer scientists at IBM. They needed a more human-friendly way to represent binary numbers in early computer systems.
Binary in Nature
Binary isn't just for computers! Many natural systems use binary-like states: on/off, true/false, yes/no. Even our genetic code uses a base-4 system that's similar to binary.
Space Communication
NASA spacecraft use hexadecimal in their communication systems. The Voyager probes, now in interstellar space, use hexadecimal codes to transmit data back to Earth.
Colorful Numbers
Every color you see on a computer screen is represented by hexadecimal values. For example, #FFFFFF is white, #000000 is black, and #FF0000 is pure red.





