Nonlinear Functions - Definition, Examples, Quiz, FAQ, Trivia

Learn how curved graphs work with fun examples and interactive activities

Educational Standards

Common Core: 8.F.A.3, 8.F.B.5, F-LE.A.1, F-LE.A.2

Learning Sections

What is Nonlinear? Types of Functions Identify Functions Examples & Graphs Real Life Examples Practice Quiz FAQs Math Trivia

What is a Nonlinear Function?

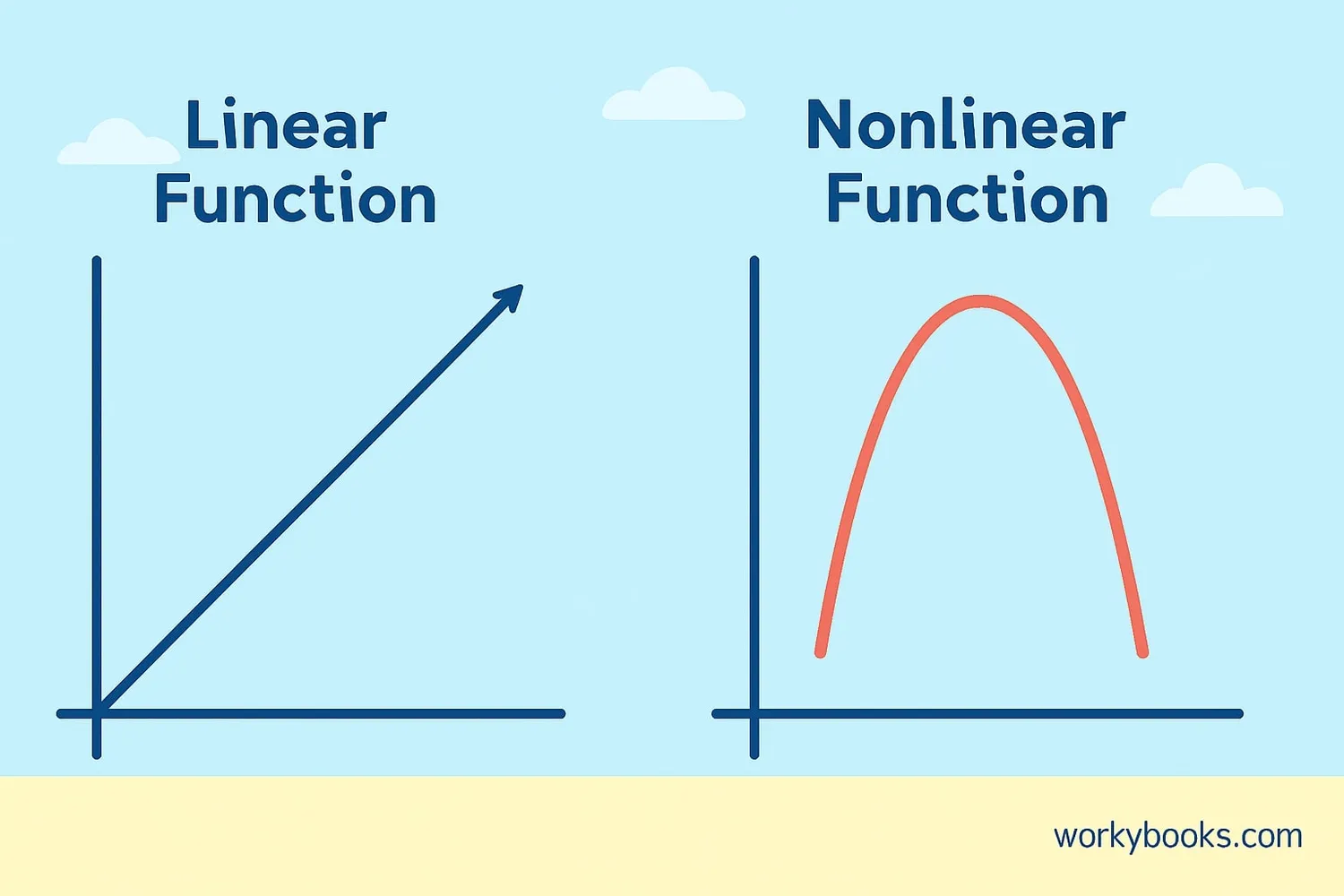
Comparing linear and nonlinear functions

A nonlinear function is like a roller coaster for numbers - instead of going in a straight line, it curves, bends, or changes direction! Unlike linear functions that make straight lines, nonlinear functions create curves when you graph them.

Key differences:
• Linear functions have a constant rate of change (like climbing stairs at the same pace)
• Nonlinear functions have changing rates (like running fast then slowing down)

In math terms, nonlinear functions have variables raised to powers (like x²), multiplied together (like x·y), or in exponents (like 2ˣ). They make the world more interesting because most things in nature aren't perfectly straight!

Key Concept

Nonlinear functions don't form straight lines when graphed. Their graphs curve, bend, or change direction!

Types of Nonlinear Functions

Quadratic

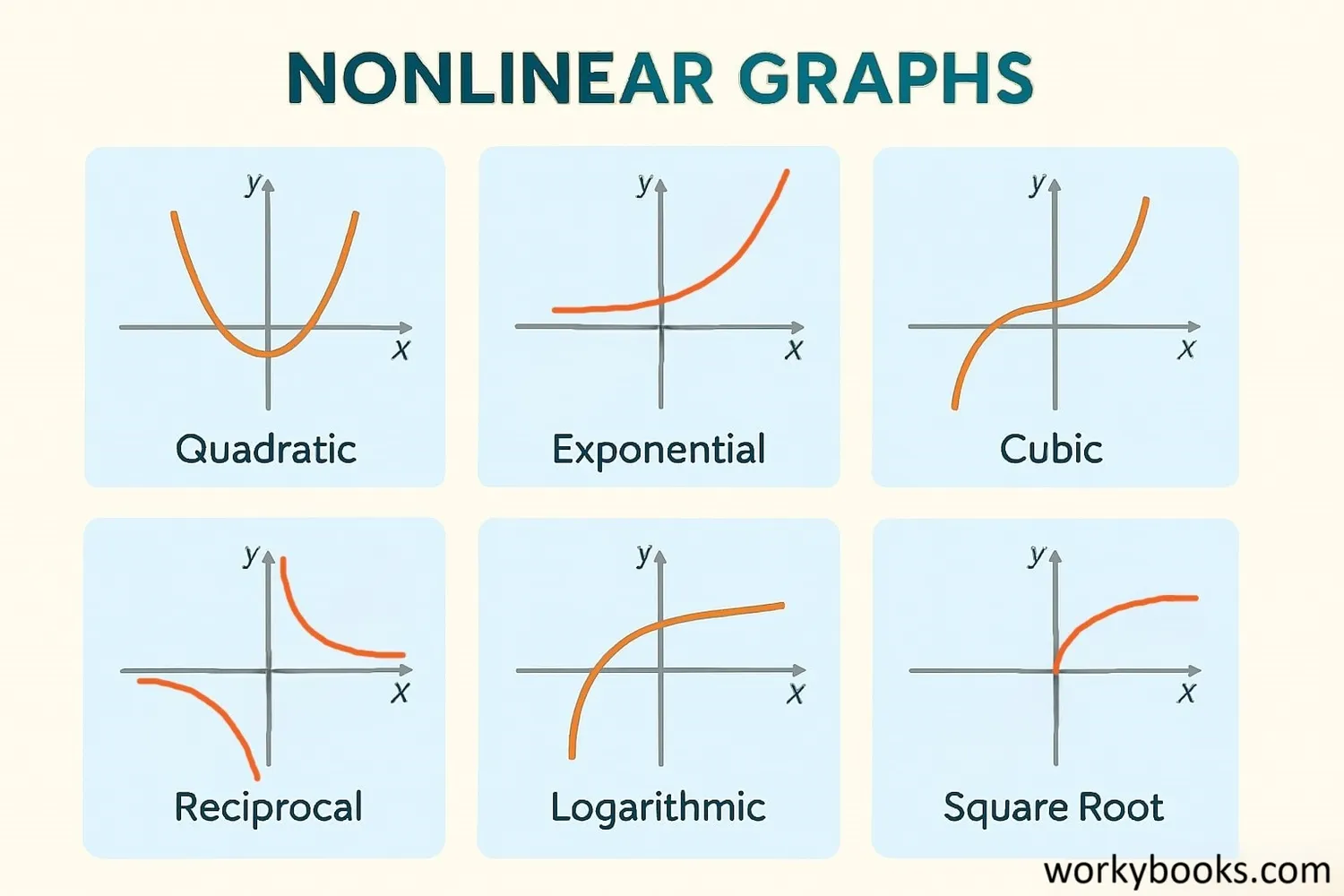
Forms a U-shaped parabola. Equation: y = ax² + bx + c

Example: y = x²

Exponential

Grows very quickly. Equation: y = a·bˣ

Example: y = 2ˣ

Cubic

Has an S-shaped curve. Equation: y = ax³ + bx² + cx + d

Example: y = x³

Logarithmic

Grows slowly. Equation: y = log_b(x)

Example: y = log(x)

Inverse Variation

One value increases while the other decreases. Equation: y = k/x

Example: y = 1/x

Polynomial

Can have many curves. Equation: y = a_nxⁿ + ... + a₁x + a₀

Example: y = x⁴ - 2x²

How to Identify Nonlinear Functions

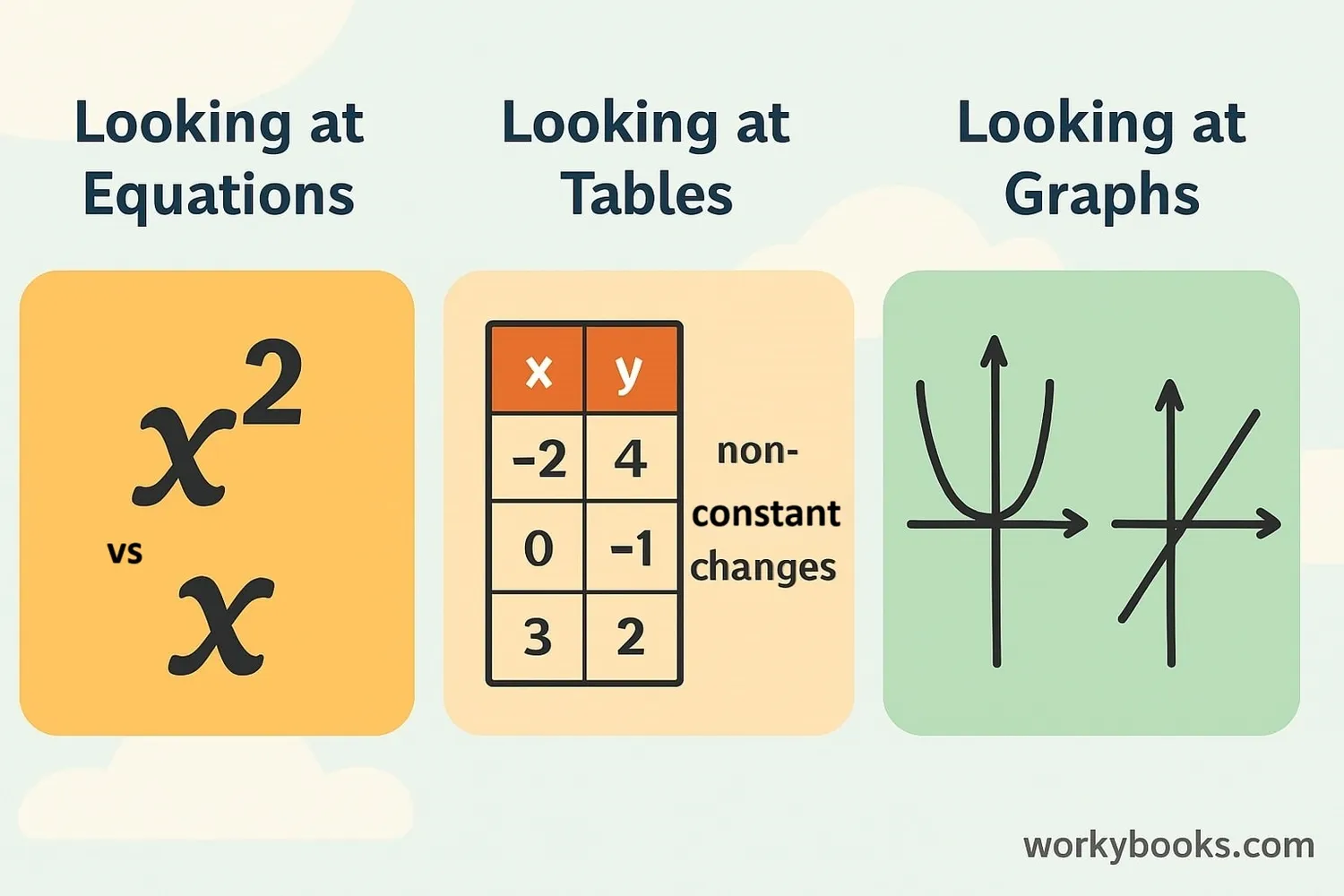
You can spot nonlinear functions in three different ways:

1. Look at the equation:
• If you see exponents (like x² or 2ˣ)
• If variables are multiplied together (like x·y)
• If there's a square root (√x) or logarithm (log x)

2. Look at a table of values:
• Calculate the rate of change between points
• If the rate isn't constant → nonlinear!

3. Look at the graph:
• If it's NOT a straight line → nonlinear!

Practice Tip

Try making a table of values for y = x². Notice how the differences between y-values aren't constant? That's a clue it's nonlinear!

Examples & Graphs

Let's look at some common nonlinear functions and their graphs:

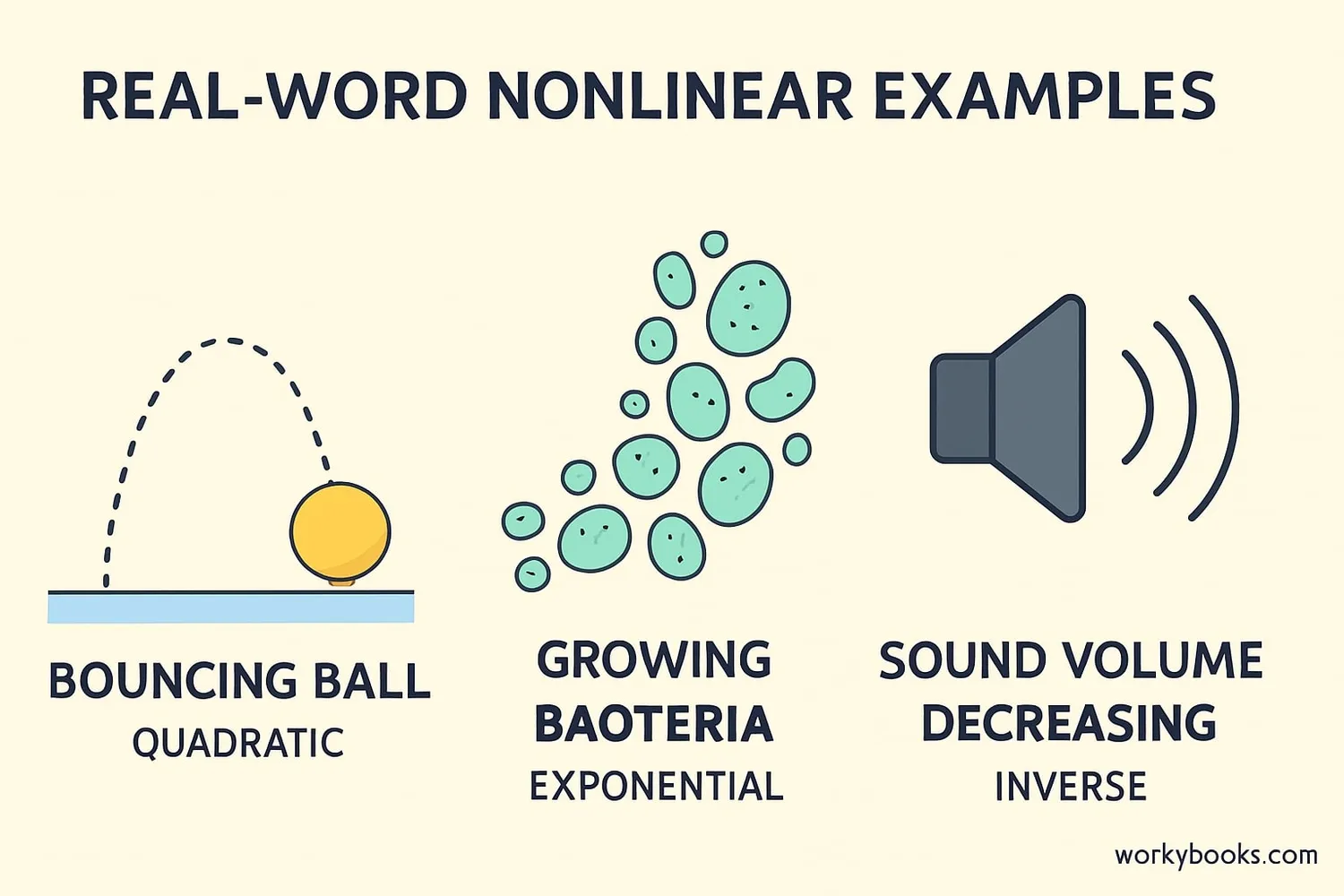
Quadratic Example: y = x²
• Graph: U-shaped parabola
• Real world: Path of a basketball shot

Exponential Example: y = 2ˣ
• Graph: Starts flat then curves upward steeply
• Real world: Spread of a rumor

Cubic Example: y = x³
• Graph: S-shaped curve
• Real world: Volume growing as you increase container size

Inverse Variation: y = 1/x
• Graph: Curves downward approaching both axes
• Real world: Time to complete a task vs number of helpers

Graphing Tip

When graphing nonlinear functions, create a table of values to plot points. Connect them with smooth curves instead of straight lines!

Real Life Examples

Nonlinear functions are everywhere in our world! Here are some examples:

Nature:
• The path of a thrown ball (quadratic)
• How plants grow (exponential at first)
• Spider webs (logarithmic spirals)

Daily Life:
• Phone battery charging (exponential)
• Braking distance of a car (quadratic)
• How loudness changes with distance (inverse)

Science:
• Planetary orbits (elliptical - nonlinear)
• Radioactive decay (exponential)
• Pendulum motion (trigonometric - nonlinear)

Did You Know?

Your heartbeat follows a nonlinear pattern - it speeds up and slows down throughout the day!

Nonlinear Functions Quiz

Test your knowledge with this 5-question quiz. Choose the correct answer for each question.

1. Which of these is a nonlinear function?

y = 3x + 2

y = x² - 4

y = 5

y = ½x

2. What shape does a quadratic function make?

Straight line

U-shaped curve

Wavy line

Zig-zag pattern

3. How can you identify a nonlinear function from a table?

The x-values are in order

The rate of change is constant

The rate of change is NOT constant

All y-values are positive

4. Which real-world example shows an exponential function?

A car driving at constant speed

Money growing with compound interest

A seesaw moving up and down

Water filling a glass at constant rate

5. Which equation represents inverse variation?

y = 3x

y = 2x²

y = 1/x

y = 5ˣ

Math Master! You've shown excellent understanding of nonlinear functions!

Good effort! Review the concepts and try again.

Frequently Asked Questions

Here are answers to common questions about nonlinear functions:

Why are nonlinear functions important?

Nonlinear functions help us model real-world phenomena that don't follow straight-line patterns. From how populations grow to how planets move, most natural processes are nonlinear. Understanding them helps scientists, engineers, and economists make accurate predictions.

Can a function be both linear and nonlinear?

No, a function is either linear or nonlinear. Linear functions always make straight lines when graphed, while nonlinear functions make curves. The simplest linear function is y = mx + b, and any function that can't be written this way is nonlinear.

Are all curved graphs nonlinear functions?

Yes! If a graph has any curve at all, it represents a nonlinear function. The only graphs that represent linear functions are perfectly straight lines. Even a very slight curve means the relationship is nonlinear.

What's the difference between nonlinear equations and nonlinear functions?

A nonlinear function describes a relationship between variables (like y = x²), while a nonlinear equation is any equation that isn't linear (like x² + y² = 25). All nonlinear functions involve nonlinear equations, but not all nonlinear equations represent functions.

Math Trivia

Discover fascinating facts about nonlinear functions:

Ancient Curves

The ancient Greeks studied nonlinear curves like parabolas and ellipses over 2000 years ago! Archimedes wrote about parabolas around 250 BC.

Butterfly Effect

Some nonlinear systems show "chaos theory" where tiny changes lead to big differences. This is called the butterfly effect - where a butterfly flapping its wings might cause a tornado weeks later!

Space Travel

NASA uses nonlinear functions to calculate rocket trajectories. Getting to the Moon requires solving complex nonlinear equations to account for gravity's changing effects!

Million-Dollar Equations

Some nonlinear equations are so complex that the Clay Mathematics Institute offers $1 million to anyone who can solve them! These are called the Millennium Prize Problems.

Related Resources

Animal Body Parts and Their Functions

In this 'Animal Body Parts and Their Functions' word sort activity aligned with LS1.A, students lear...

Shape and Function Match

Shape and Function Match' helps students explore how specific shapes, like wheels or screws, aid obj...

Plant Parts Function Sort

This classification activity helps students understand how different plant structures contribute to ...

Golgi Apparatus and Its Function

This NGSS-aligned reading passage introduces middle school students to the structure and function of...

The Nucleolus and Its Function

This NGSS-aligned reading passage focuses on the nucleolus, a key structure inside the cell’s nucleu...

Parts of Speech Functions in Sentences

Ribosomes Function

Parts of the Cell

This informational science passage, aligned with NGSS standard MS-LS1-1, introduces students to the ...

Animal Structures Word Sort

This engaging classification activity helps students understand the different structures that make u...

Nonlinear Functions - Definition, Examples, Quiz, FAQ, Trivia