Direct Variation - Definition, Examples, Quiz, FAQ, Trivia
Learn about proportional relationships with simple explanations, examples, and practice activities
What is Direct Variation?

Direct variation describes a simple relationship between two quantities: when one quantity increases, the other increases at a constant rate. Similarly, when one decreases, the other decreases at that same constant rate.
For example, think about buying apples at the grocery store. If each apple costs 50 cents, then:
- 1 apple costs 50 cents
- 2 apples cost 100 cents
- 3 apples cost 150 cents
Key Characteristics
Direct variation always passes through (0,0) - if you have zero of one thing, you have zero of the other.
The Direct Variation Formula
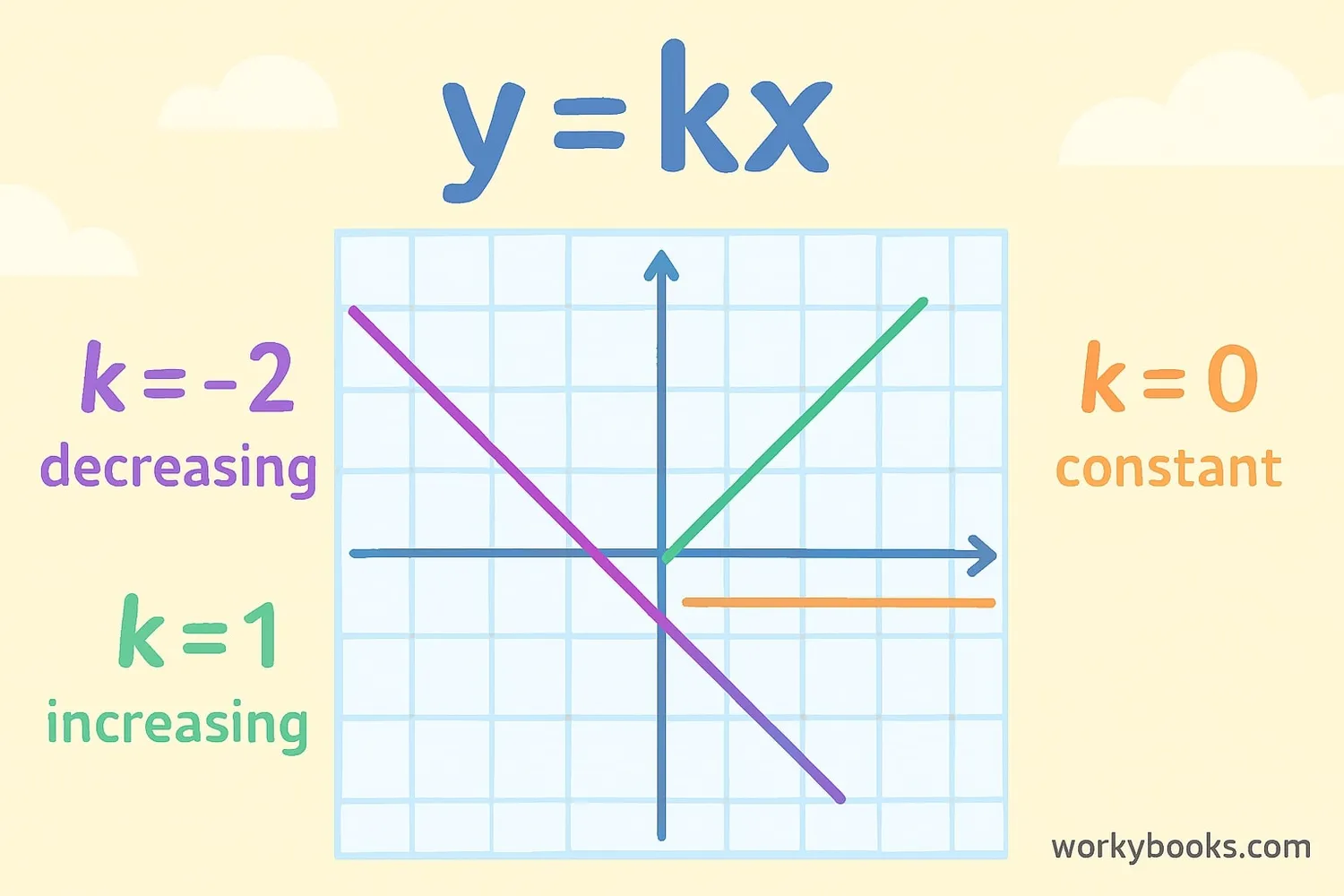
We can express direct variation with a simple formula:
Direct Variation Formula
Where:
- y is the dependent variable (the result)
- x is the independent variable (what you change)
- k is the constant of proportionality
Let's find k for this situation:
| Apples (x) | Cost in cents (y) |
|---|---|
| 1 | 50 |
| 2 | 100 |
| 3 | 150 |
| 4 | 200 |
Remember
The constant of proportionality (k) never changes in a direct variation relationship. It's the same for every pair of (x,y) values.
The Direct Variation Graph
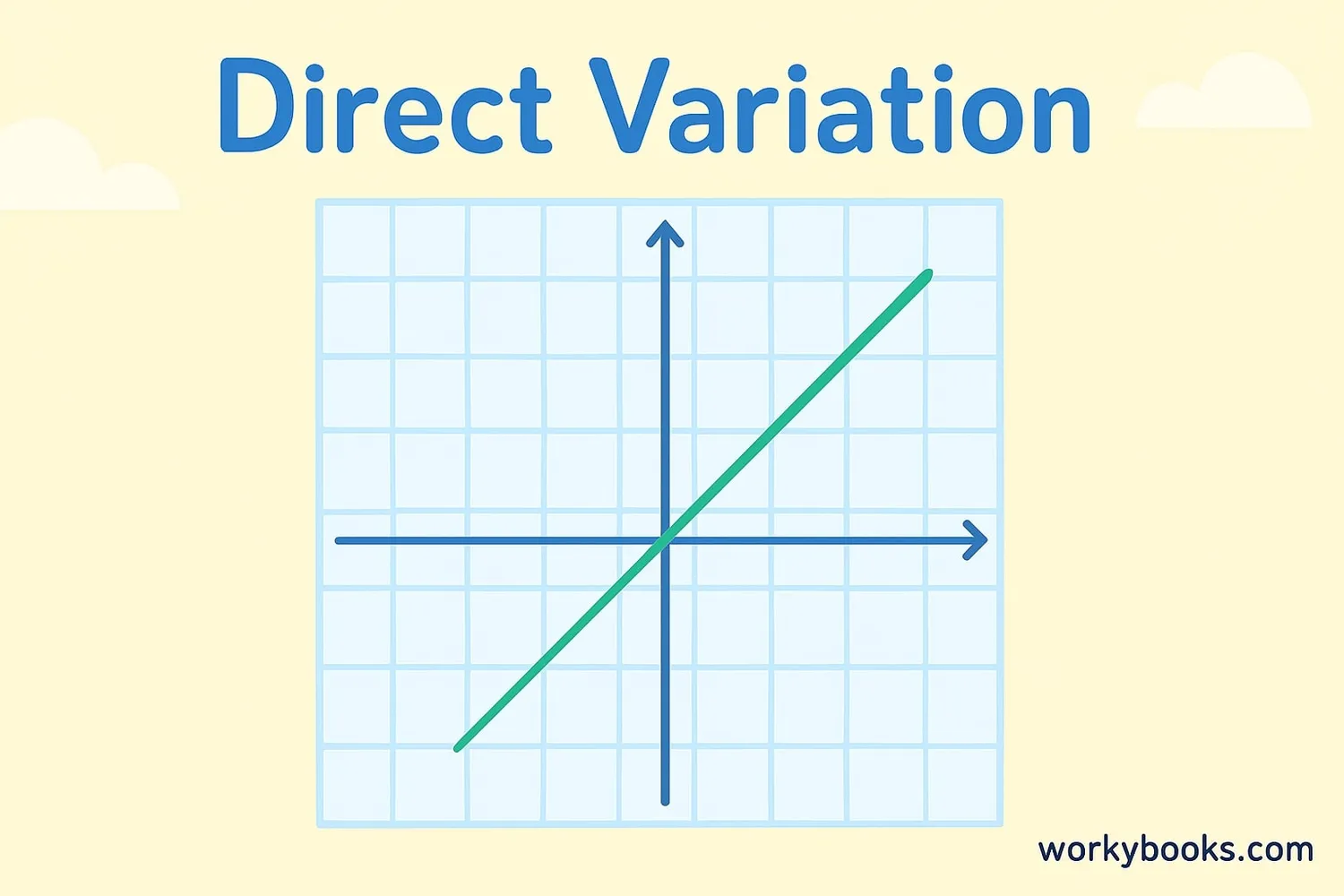
The graph of a direct variation relationship is always a straight line that passes through the origin (0,0). The slope of this line is equal to k, the constant of proportionality.
Characteristics of the graph:
- Always starts at (0,0) - if x=0, then y=0
- Straight line (never curves)
- Slopes upward (positive k) or downward (negative k)
- The steeper the slope, the larger the constant k
| k value | Graph appearance |
|---|---|
| k = 1 | Line at 45° angle |
| k = 2 | Steeper line (rises faster) |
| k = 0.5 | Flatter line (rises slower) |
| k = -1 | Downward line at 45° angle |
Graph Tip
If a line doesn't pass through (0,0), it's not direct variation! It might be a different type of relationship.
Solving Direct Variation Problems
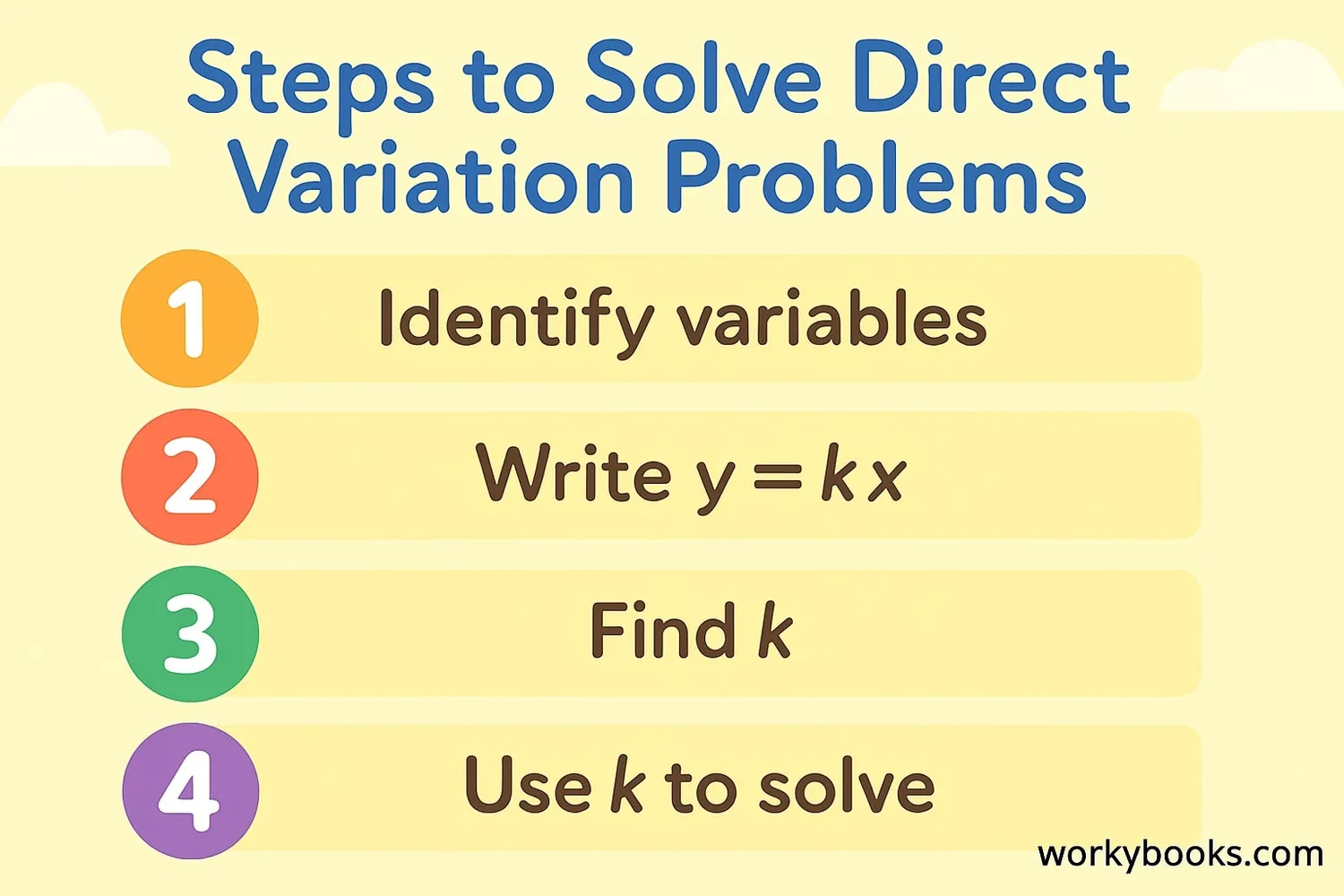
Let's learn how to solve direct variation problems step by step:
Example Problem: If y varies directly with x, and y = 15 when x = 3, what is y when x = 7?
Step 1: Write the direct variation formula: y = kx
Step 2: Plug in the values we know to find k:
15 = k × 3
Step 3: Solve for k: k = 15 ÷ 3 = 5
Step 4: Now use k to find y when x = 7: y = 5 × 7 = 35
So when x = 7, y = 35.
Another Example: The distance a car travels varies directly with time. In 2 hours, it travels 120 miles. How far will it travel in 5 hours?
Solution:
- Distance = k × Time
- 120 = k × 2 → k = 60 miles per hour
- Distance = 60 × 5 = 300 miles
Problem Solving Tip
Always start by writing y = kx, then find k using the values you know, then use k to find the unknown value.
Real Life Examples
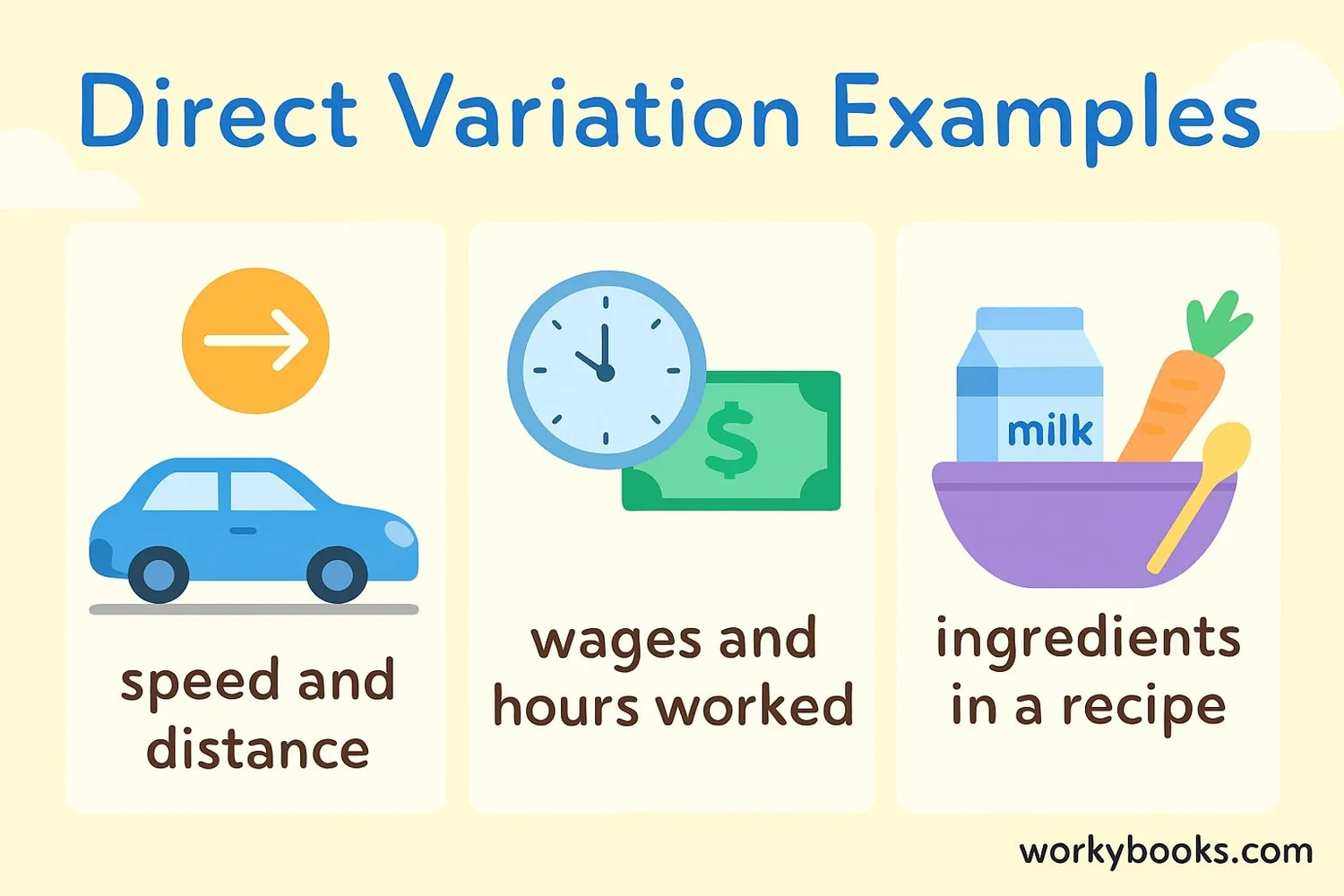
Direct variation is all around us! Here are common examples:
1. Wages: Money earned = hourly rate × hours worked
If you earn $10 per hour, your earnings vary directly with hours worked.
2. Travel: Distance = speed × time
At constant speed, distance varies directly with time.
3. Recipes: Ingredients = servings × amount per serving
If a cookie recipe needs 2 cups of flour for 12 cookies, then for 24 cookies you need 4 cups.
4. Shopping: Total cost = price per item × number of items
The more items you buy, the higher the total cost.
5. Geometry: Circumference = π × diameter
For any circle, circumference varies directly with diameter.
Real World Connection
Notice how many real-life situations follow this simple pattern? That's why understanding direct variation is so useful!
Practice Quiz
Test your understanding with these 5 questions. Choose the correct answer for each.
Frequently Asked Questions
Here are answers to common questions about direct variation:
Math Trivia
Discover interesting facts about proportional relationships:
Ancient Origins
The concept of proportionality dates back to ancient Greek mathematicians like Euclid and Pythagoras. They used proportional relationships in geometry and music theory.
In Nature
Many natural phenomena follow direct variation. For example, the distance a spring stretches is directly proportional to the force applied (Hooke's Law in physics).
Space Exploration
NASA engineers use direct variation to calculate fuel needs. The fuel required for a rocket is directly proportional to the distance it needs to travel.
Golden Ratio
The famous Golden Ratio (1.618) represents a special proportional relationship found in art, architecture, and nature. It's considered aesthetically pleasing.





