Function Notation - Definition, Examples, Quiz, FAQ, Trivia
Learn how functions work with f(x) notation through simple explanations and practice activities
What is Function Notation?
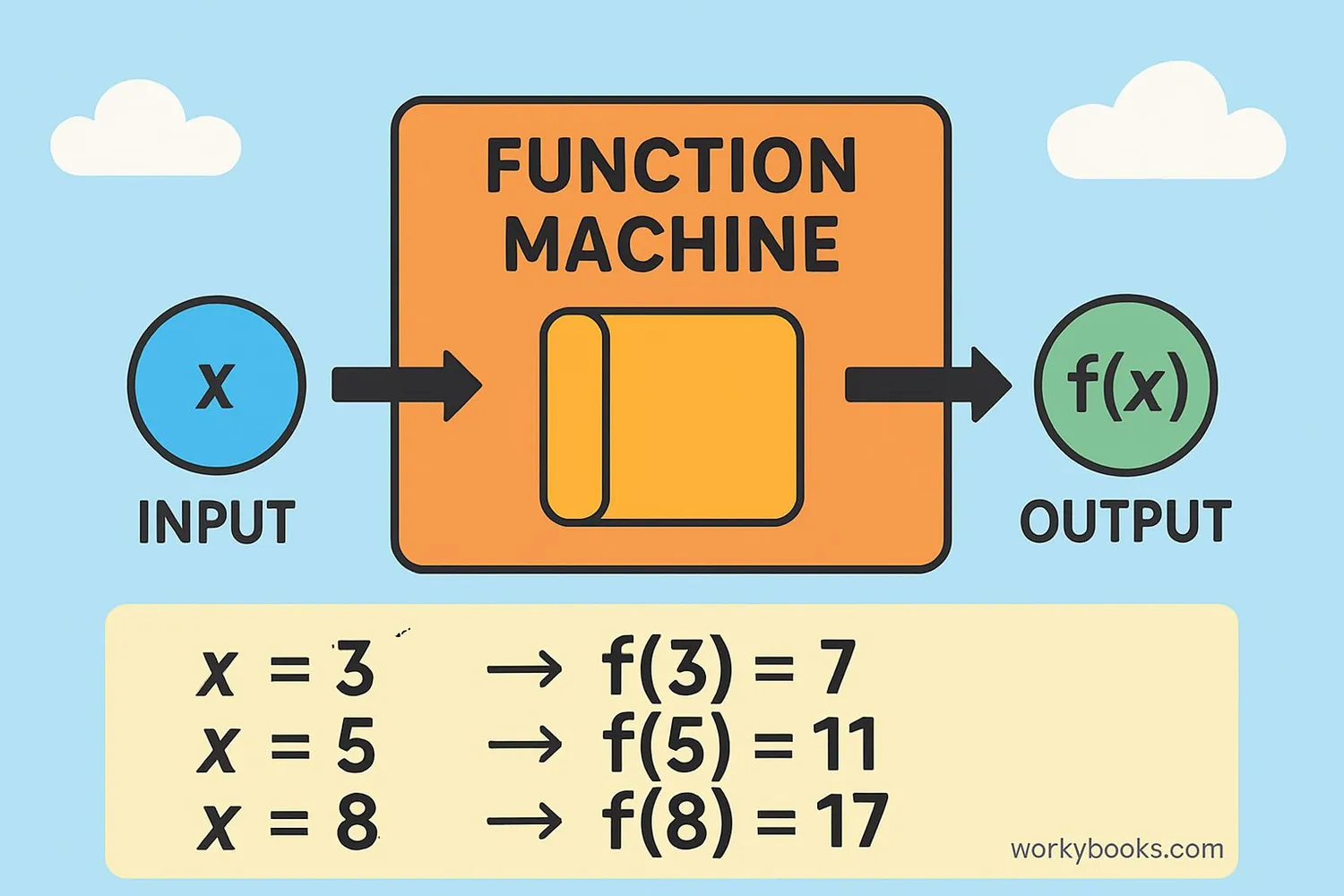
Function notation is a special way to write mathematical relationships. Instead of writing y = 2x + 1, we can write f(x) = 2x + 1. The "f" stands for function, and the "(x)" tells us that x is the input value.
Think of a function as a special math machine. You put a number into the machine, it follows a rule, and gives you back a different number. The notation f(x) is how we name this machine and describe what it does.
Why is this useful? Function notation helps us:
- Clearly show which rule we're using
- Easily substitute different input values
- Work with multiple functions (like g(x), h(x))
- Understand how inputs relate to outputs
Key Concept
f(x) is read as "f of x" and means "the output of function f when the input is x".
How to Use Function Notation

Using function notation involves two main skills: defining functions and evaluating functions.
Function Definition
This defines the rule that the function follows.
Function Evaluation
Replace x with the input value and calculate.
Example: For f(x) = 3x - 2
Step 1: To find f(4), replace x with 4 → f(4) = 3(4) - 2
Step 2: Calculate → 12 - 2 = 10
Step 3: So f(4) = 10
This means when we put 4 into the function, we get 10 out.
Function Machine Example
f(x) = x² + 2
Input (x)
2
Function
f(2) = 2² + 2
Output
6
Function Notation Examples

Let's explore some practical examples of function notation:
Example 1: Temperature Conversion
The function to convert Celsius to Fahrenheit is:
F(C) = (9/5)C + 32
What is 20°C in Fahrenheit?
F(20) = (9/5)(20) + 32 = 36 + 32 = 68°F
Example 2: Speed Calculation
Distance traveled at constant speed: d(t) = 60t
How far do you travel in 3 hours at 60 mph?
d(3) = 60 × 3 = 180 miles
Example 3: Baking Cookies
Cookies needed for guests: c(g) = 3g + 6
How many cookies for 4 guests?
c(4) = 3(4) + 6 = 12 + 6 = 18 cookies
Example 4: Multiple Functions
g(x) = x + 5
h(x) = 2x - 3
Find g(4) + h(2)
g(4) = 4 + 5 = 9
h(2) = 2(2) - 3 = 1
9 + 1 = 10
Remember
The letter before the parentheses (f, g, h) is the function name. The value inside the parentheses is the input.
Function Notation Quiz
Test your understanding of function notation with this 5-question quiz.
Frequently Asked Questions
Here are answers to common questions about function notation:
Math Trivia
Discover interesting facts about functions and mathematics:
Origin of f(x)
The notation f(x) was first used by Swiss mathematician Leonhard Euler in the 18th century. He's considered one of the greatest mathematicians of all time.
Functions in Nature
Many natural patterns follow mathematical functions. The spiral of a seashell follows a function called the Fibonacci sequence, and the path of a falling object follows a quadratic function.
Space Travel
Functions are essential for space travel. Rocket scientists use functions to calculate trajectories, orbital paths, and fuel requirements. A small error in these functions could send a spacecraft off course!
Most Complex Function
The Riemann zeta function is one of the most complex and important functions in mathematics. Solving it completely could win a $1 million prize from the Clay Mathematics Institute!





