Inverse Functions - Definition, Examples, Quiz, FAQ, Trivia
Learn how functions can undo each other with easy explanations and practice activities
What is an Inverse Function?
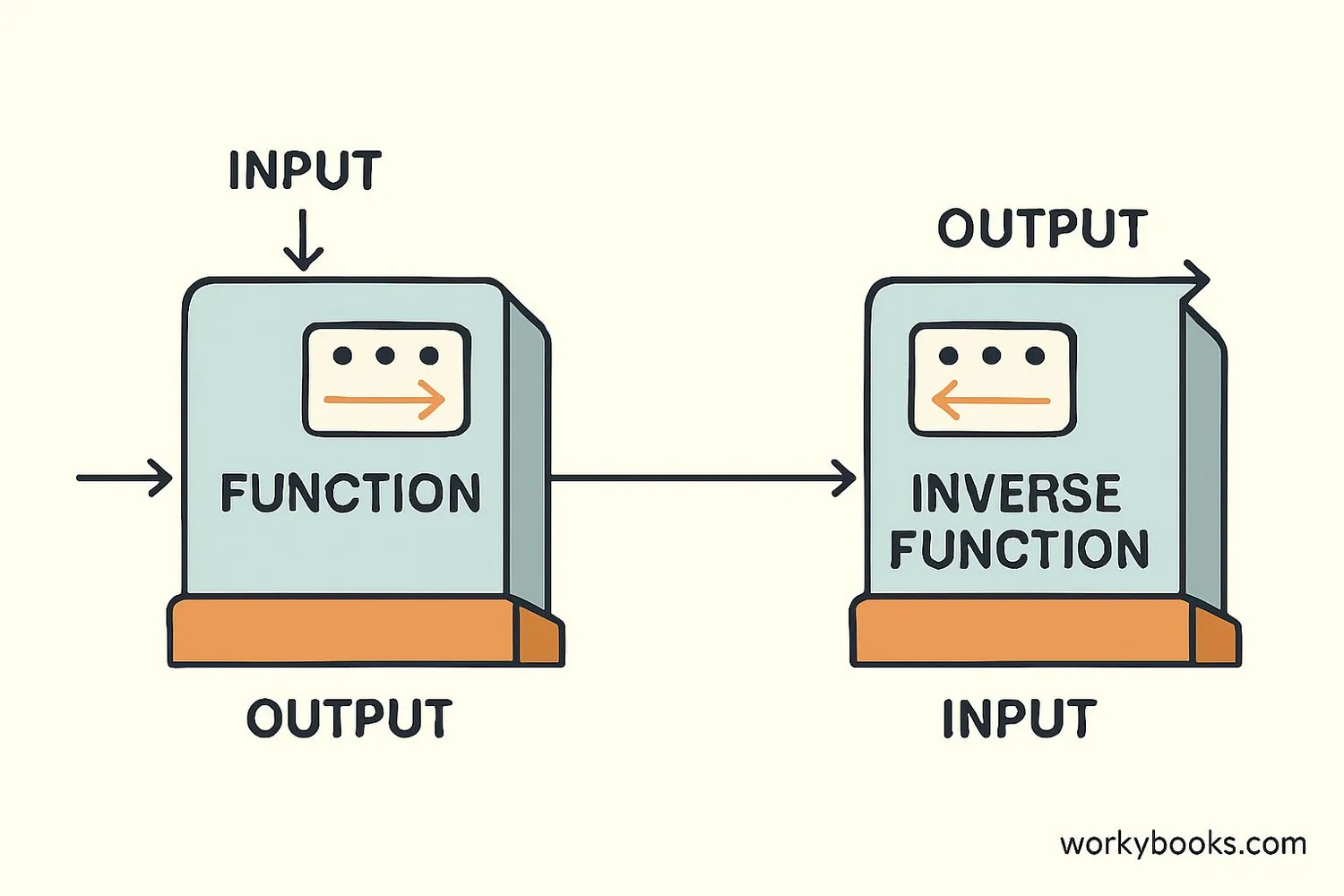
An inverse function is like a mathematical undo button! Just like you can put on your shoes and then take them off, inverse functions do opposite operations.
If a function does something to a number, its inverse function reverses that action. For example, if a function adds 5 to a number, its inverse would subtract 5.
For a function to have an inverse, each input must go to exactly one output, and each output must come from exactly one input. This is called a "one-to-one" function.
Key Concept
Inverse functions reverse each other. If f(x) is a function, its inverse is written as f⁻¹(x). When you apply both, you get back to where you started: f⁻¹(f(x)) = x.
How to Find the Inverse of a Function
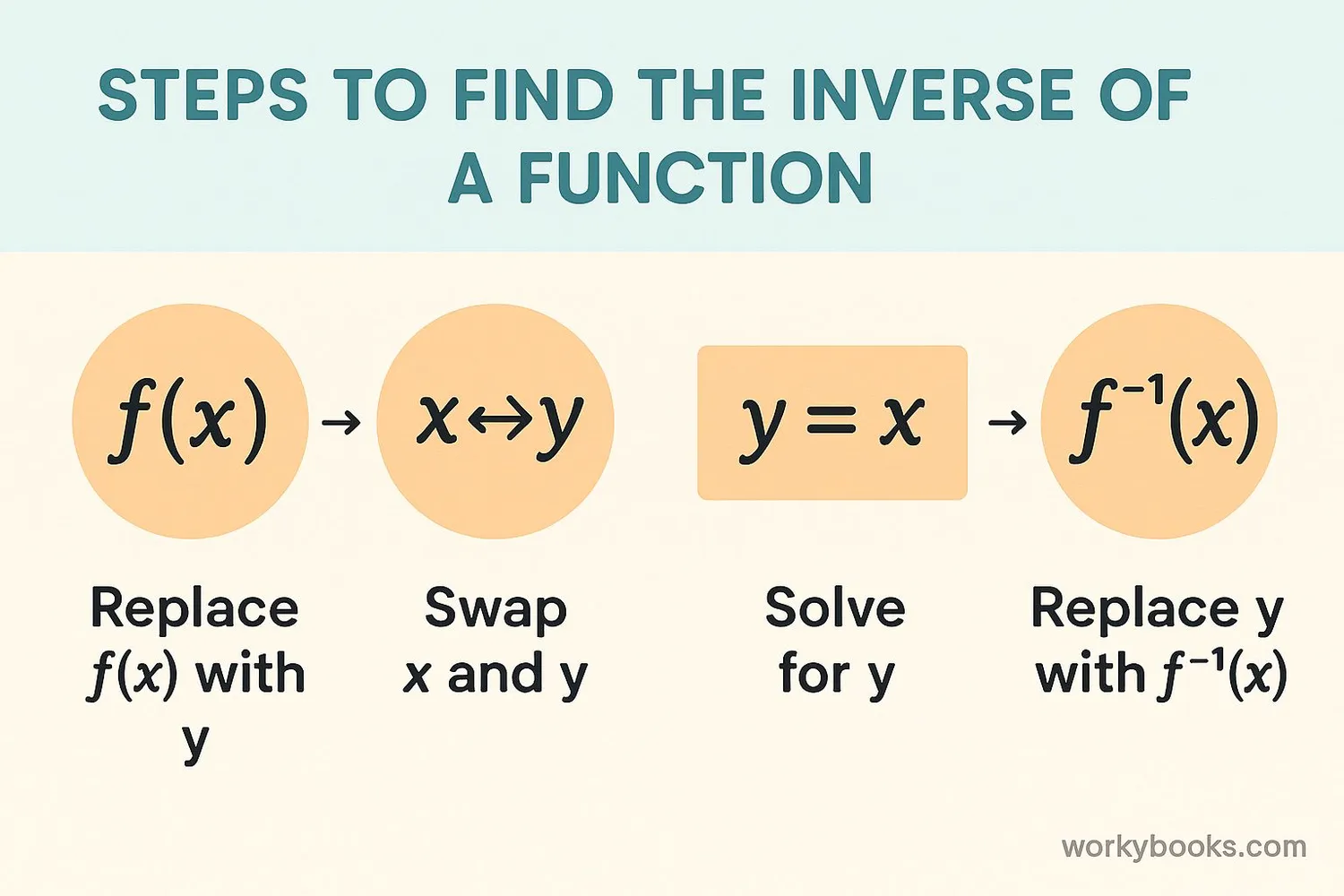
Finding the inverse of a function follows a simple process:
Steps to Find an Inverse
- Replace f(x) with y
- Swap x and y in the equation
- Solve the new equation for y
- Replace y with f⁻¹(x)
Example: Find the inverse of f(x) = 2x + 3
Step 1: y = 2x + 3
Step 2: x = 2y + 3 (swapped x and y)
Step 3: x - 3 = 2y → y = (x - 3)/2 (solved for y)
Step 4: f⁻¹(x) = (x - 3)/2
Now we can check: f(5) = 2×5 + 3 = 13, and f⁻¹(13) = (13-3)/2 = 5. It works!
Remember
Not all functions have inverses. Only one-to-one functions (where each output comes from exactly one input) have inverses.
Graph of Inverse Function
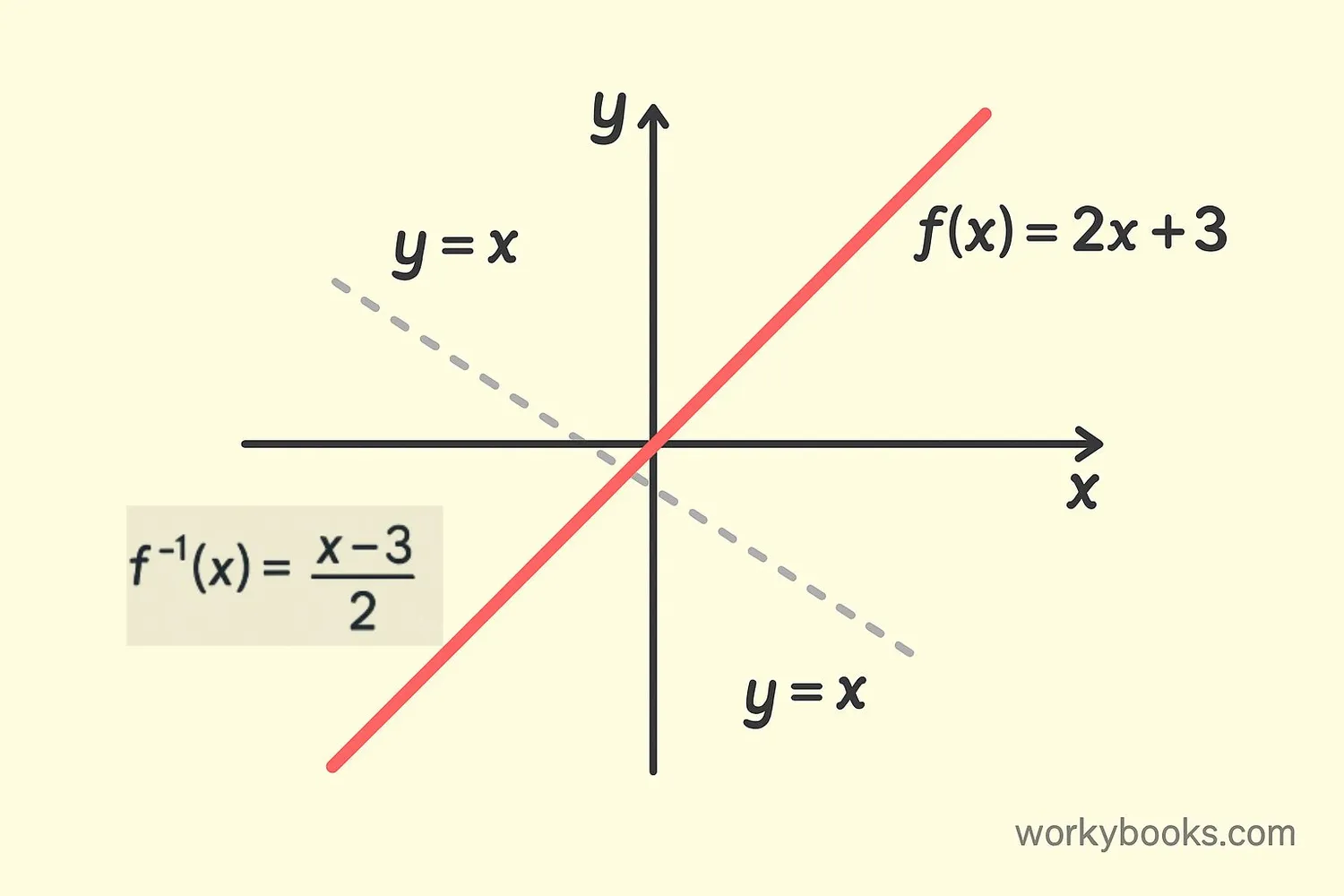
The graphs of a function and its inverse have a special relationship—they are mirror images across the line y = x.
This means if you fold the graph along the line y = x, the function and its inverse would match up perfectly.
You can use this property to graph an inverse function without even finding its equation—just reflect the original graph across the line y = x.
Graph Tip
If a function and its inverse are the same, the function is symmetric about the line y = x. The function f(x) = x is its own inverse!
Inverse Function Examples
Let's look at some examples of inverse functions:
| Function | Inverse Function | Check |
|---|---|---|
| f(x) = x + 7 | f⁻¹(x) = x - 7 | f(3)=10, f⁻¹(10)=3 |
| g(x) = 3x | g⁻¹(x) = x/3 | g(4)=12, g⁻¹(12)=4 |
| h(x) = 2x - 5 | h⁻¹(x) = (x + 5)/2 | h(6)=7, h⁻¹(7)=6 |
| p(x) = x² (x≥0) | p⁻¹(x) = √x | p(9)=81, p⁻¹(81)=9 |
Notice that for p(x) = x², we had to specify x≥0. This is because without this restriction, p(x) wouldn't be one-to-one (both 3 and -3 give 9), so it wouldn't have an inverse.
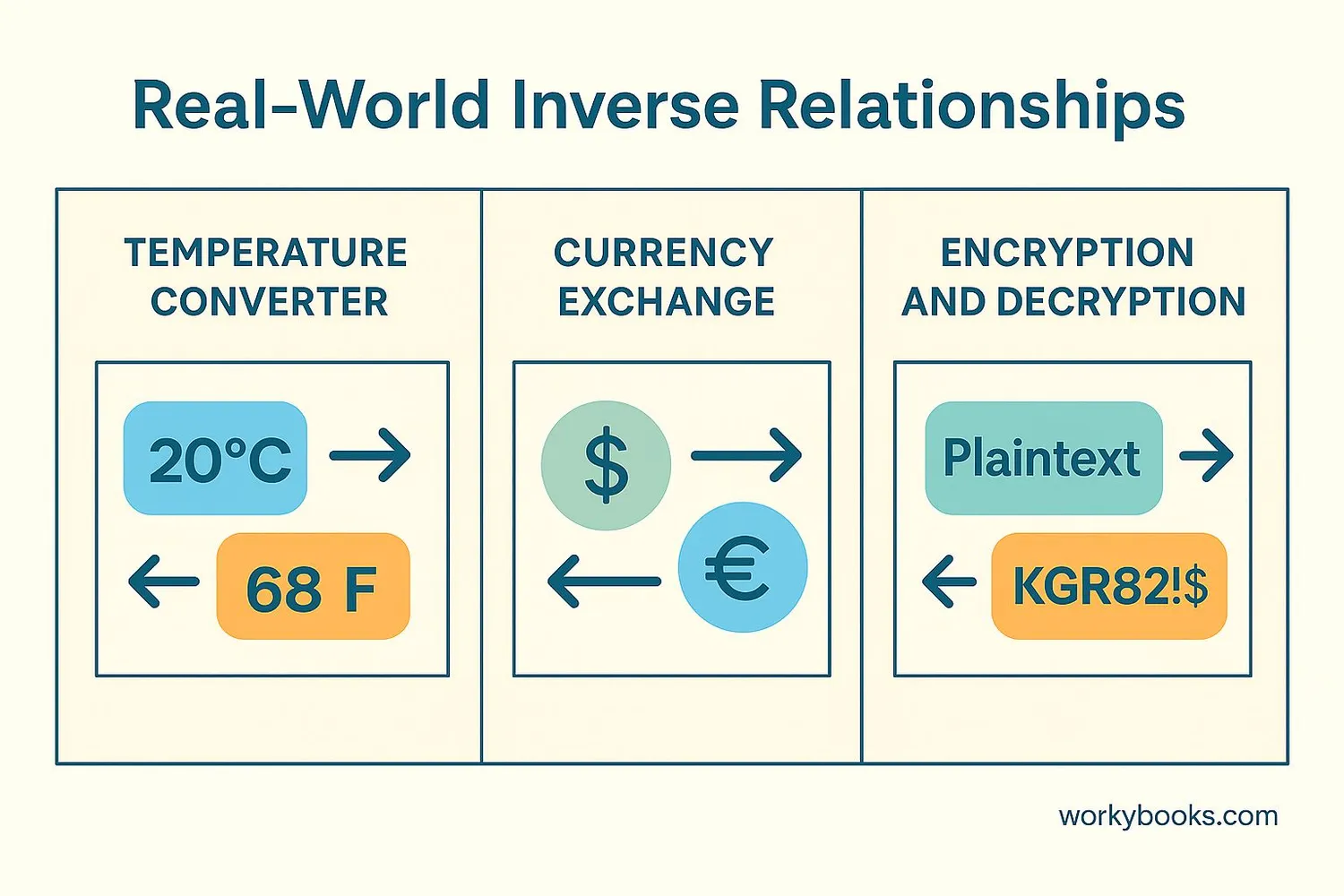
Inverse functions are all around us in daily life:
Example 1: Temperature conversion - Celsius to Fahrenheit and back
F = (9/5)C + 32 and C = (5/9)(F - 32) are inverses!
Example 2: Encryption and decryption - encoding and decoding messages
Example 3: Currency exchange - converting between dollars and euros
Real-World Connection
Many real-world processes are inverses of each other: wrapping and unwrapping gifts, locking and unlocking doors, or putting together and taking apart puzzles.
Inverse Function Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about inverse functions:
Math Trivia
Discover interesting facts about functions and mathematics:
Historical Origins
The concept of inverse functions dates back to the 17th century. Mathematicians like Gottfried Wilhelm Leibniz and Isaac Newton developed early ideas about functions and their inverses as part of developing calculus.
Real-World Applications
Inverse functions are used in cryptography to encrypt and decrypt messages. They're also essential in engineering for converting between different measurement systems and in physics for solving equations that describe motion.
Calculator Functions
Your calculator uses inverse functions! The "undo" button for many operations uses inverse functions. For example, the square root function is the inverse of squaring, and the ln (natural log) function is the inverse of eˣ.
Special Inverse
The function f(x) = 1/x is its own inverse! If you apply it twice, you get back to your original value: f(f(x)) = f(1/x) = 1/(1/x) = x. This is true for all x ≠ 0.





