Rotation in math - Definition, Examples, Quiz, FAQ, Trivia
Learn about geometric rotation with visual examples, interactive activities, and practice quizzes
What is Rotation?
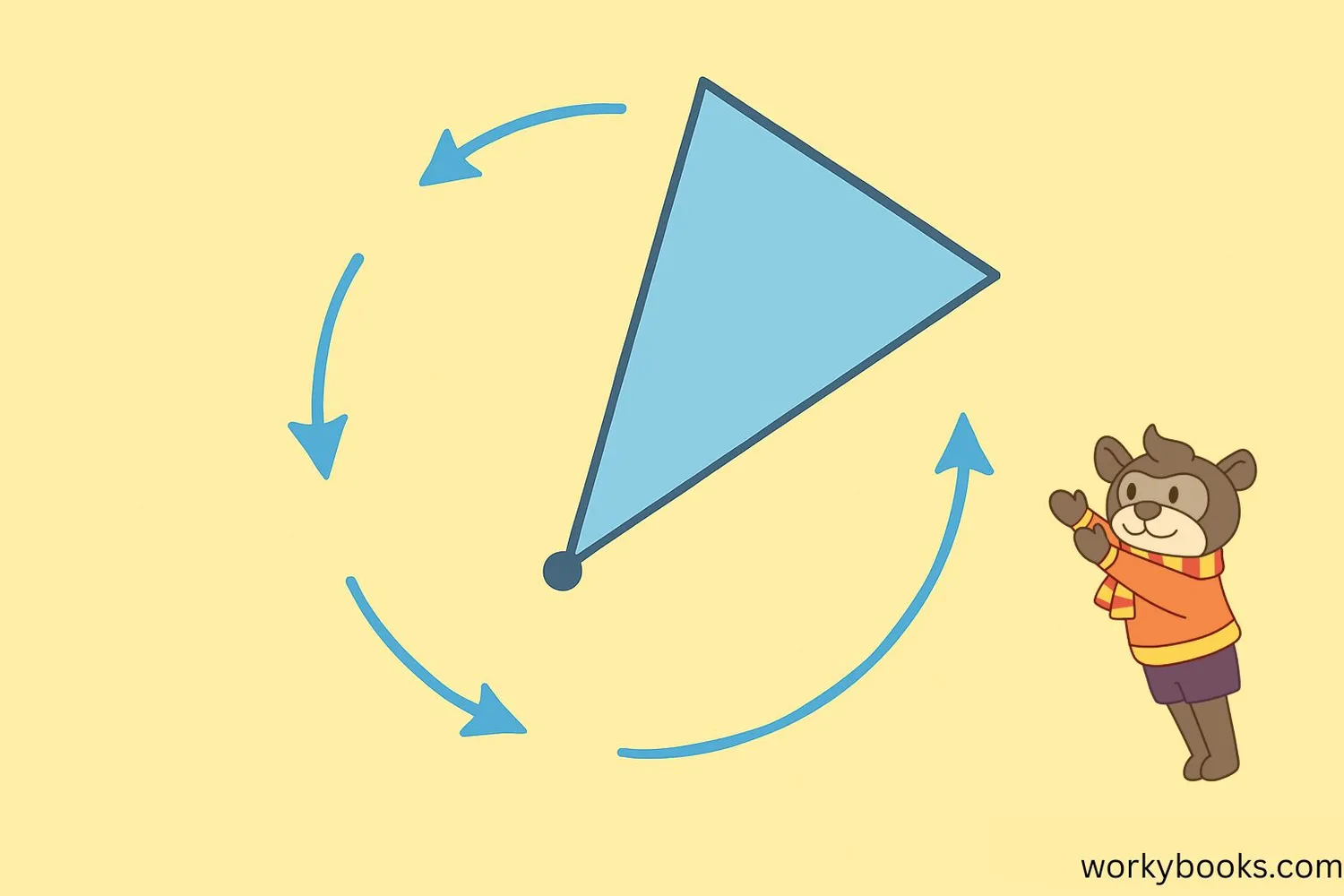
Rotation is a type of geometric transformation where a shape turns around a fixed point called the center of rotation. Think of it like spinning a toy top or turning a doorknob.
Every rotation has three important parts:
1. The center point (where the shape rotates around)
2. The angle of rotation (how far it turns)
3. The direction (clockwise or counterclockwise)
Rotation is an isometric transformation, which means the shape doesn't change size - it just changes position and orientation. Other types of transformations include translation (sliding), reflection (flipping), and dilation (resizing).
Key Concept
Rotation preserves the shape and size of an object while changing its orientation in space.
How Rotation Works
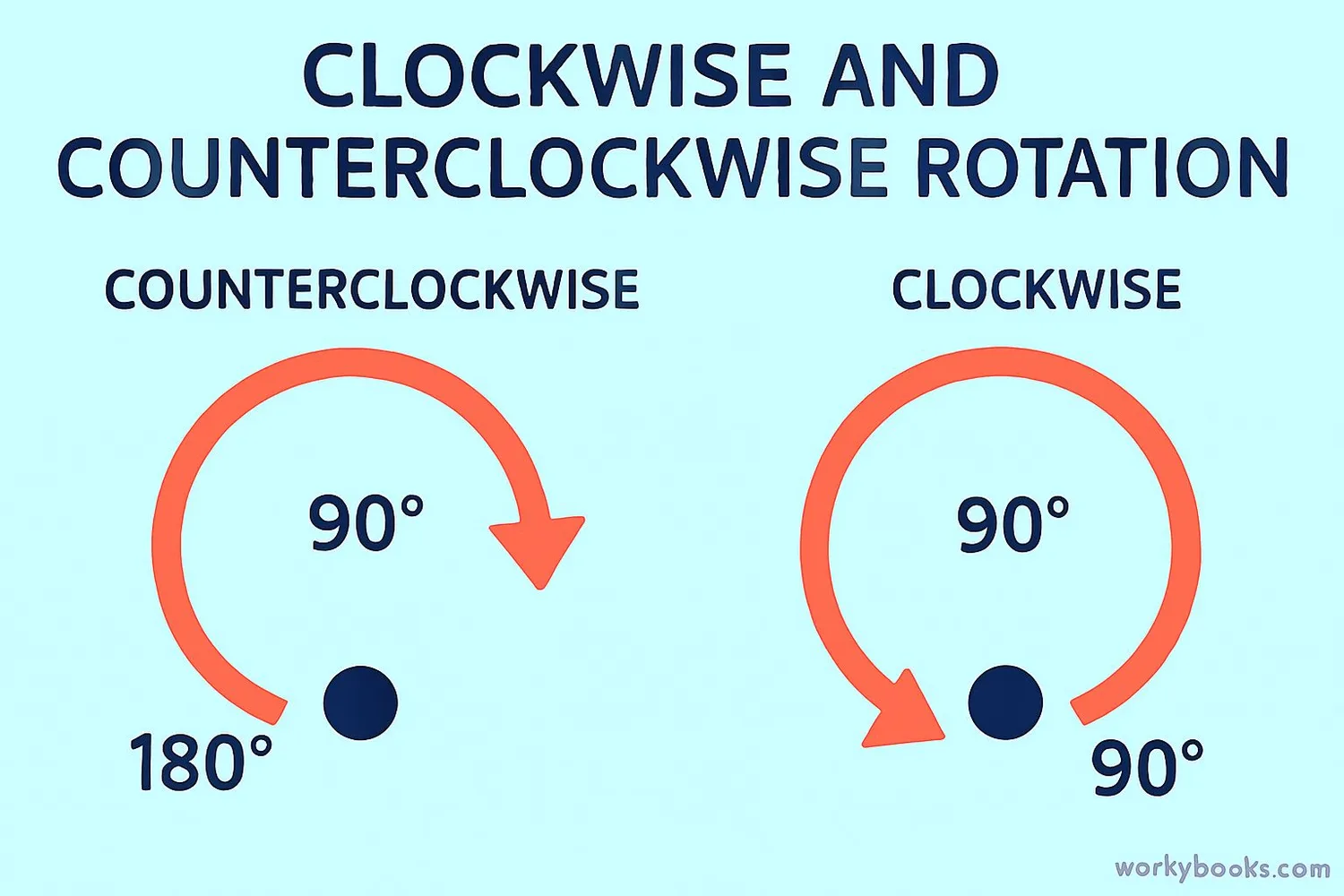
Let's understand rotation step by step:
1. Center of Rotation: This is the fixed point that everything rotates around. It can be inside the shape, on its edge, or even outside the shape.
2. Direction of Rotation:
- Clockwise (like the hands of a clock moving)
- Counterclockwise (the opposite direction)
3. Angle of Rotation: How far the shape turns. Common rotations are:
- 90° (quarter turn)
- 180° (half turn)
- 270° (three-quarter turn)
- 360° (full turn - back to start)
Rotation Rules
When rotating a point (x,y) around the origin (0,0):
Remember
A 360° rotation brings the shape back to its original position. This is called a full rotation.
Rotational Symmetry
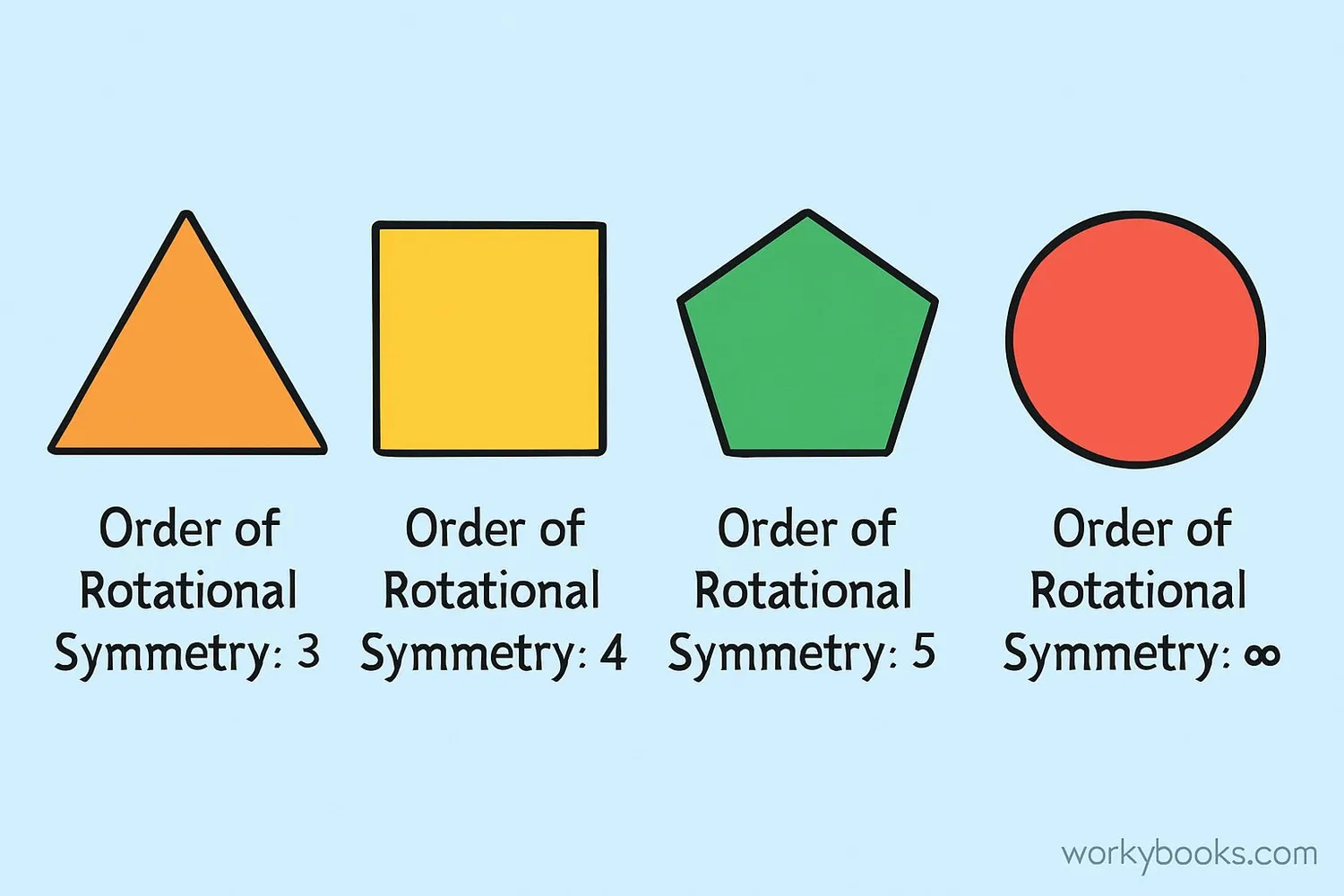
A shape has rotational symmetry if it looks exactly the same after being rotated by a certain angle. The number of times a shape matches itself during a full 360° rotation is called its order of rotational symmetry.
Examples:
- Square: Has rotational symmetry of order 4 (matches at 90°, 180°, 270°, and 360°)
- Equilateral Triangle: Order 3 (120°, 240°, 360°)
- Circle: Order infinity (looks the same at any rotation angle)
To find the rotational symmetry of a shape:
1. Find the center point
2. Rotate the shape
3. See at which angles it looks identical to the original
Fun Fact
Many real-world objects have rotational symmetry - flowers, snowflakes, stars, and wheels!
Rotation Examples
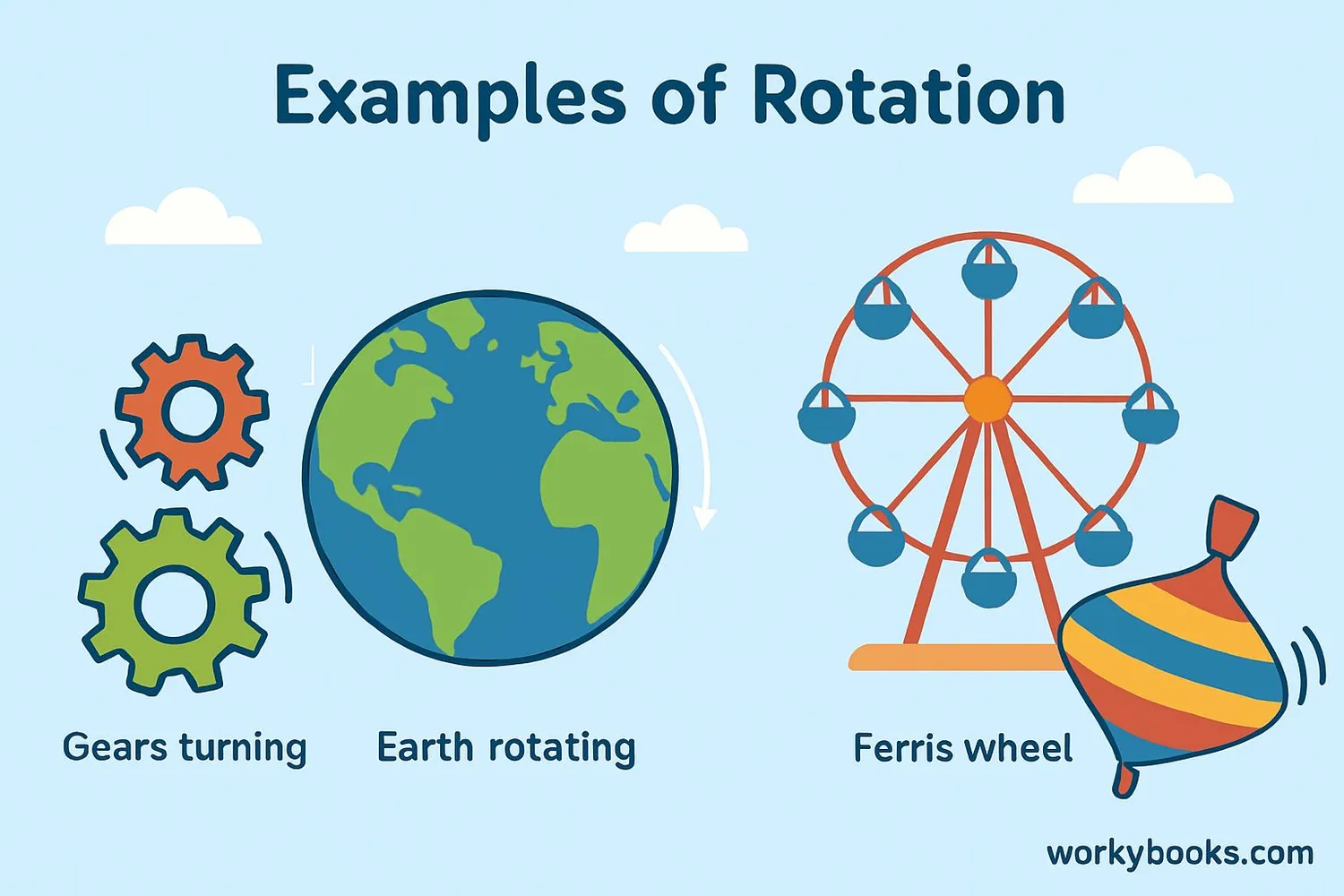
Rotation is all around us! Here are some examples:
Example 1: Clock Hands
The hands of a clock rotate around the center. The minute hand rotates 360° every hour (6° per minute).
Example 2: Earth's Rotation
Our planet rotates around its axis, causing day and night. It completes a full 360° rotation every 24 hours.
Example 3: Wheel Rotation
Wheels rotate around their center axle. A bicycle wheel rotates as you pedal, moving the bike forward.
Example 4: Rotating a Triangle
Imagine a triangle with vertices at (1,1), (3,1), and (2,3). If we rotate it 90° counterclockwise around the origin:
- (1,1) becomes (-1,1)
- (3,1) becomes (-1,3)
- (2,3) becomes (-3,2)
Math Tip
To rotate a shape on graph paper, rotate each point individually using the rotation rules, then connect the new points.
Rotation Quiz
Test your understanding of rotation with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about rotation in math:
Math Trivia
Discover interesting facts about rotation and geometry:
Ancient Rotations
The concept of rotation has been studied since ancient times. The Babylonians used rotational symmetry in their art and architecture over 4,000 years ago.
Fast Rotation
The fastest rotating man-made object is a tiny dumbbell-shaped nanoparticle that spins at an incredible 300 billion rotations per minute!
Cosmic Rotation
Our Milky Way galaxy rotates at about 210 kilometers per second (130 miles per second). It takes approximately 225-250 million years to complete one full rotation.
Rotational Symmetry Record
Snowflakes have some of the most intricate rotational symmetry in nature, typically with 6-fold symmetry due to the hexagonal structure of ice crystals.





